ทำตารางตรีโกณมิติ Sin Cos Tan (ทุกมุม) + วิธีทำความเข้าใจ

ตารางตรีโกณมิติ sin cos tan คือชุดของตารางที่มีค่าตรีโกณมิติหรือ sin cos แทนเจนต์ของมุม

บทความนี้แสดงตารางค่าตรีโกณมิติของ sin cos tan จากมุมพิเศษต่างๆตั้งแต่0ºถึง360º (หรือที่เรียกกันทั่วไปว่ามุมวงกลม 360 องศา) ดังนั้นคุณจึงไม่ต้องกังวลกับการจำอีกต่อไป

สำหรับสูตรเอกลักษณ์ตรีโกณมิติคุณสามารถอ่านได้ในบทความนี้

คำจำกัดความของ Sin Cos Tan

ก่อนที่จะเข้าสู่ตารางของค่าตรีโกณมิติคุณควรทำความเข้าใจคำว่าตรีโกณมิติและ sin cos tan ก่อน

• ตรีโกณมิติเป็นสาขาหนึ่งของคณิตศาสตร์ที่ศึกษาความสัมพันธ์ระหว่างความยาวและมุมของสามเหลี่ยม
• Sin (ไซน์)คืออัตราส่วนของความยาวในรูปสามเหลี่ยมระหว่างด้านหน้าของมุมและด้านตรงข้ามมุมฉาก y / z
• Cos (โคไซน์)คืออัตราส่วนของความยาวในรูปสามเหลี่ยมระหว่างด้านของมุมกับด้านตรงข้ามมุมฉาก x / z
• Tan (แทนเจนต์)คืออัตราส่วนของความยาวในรูปสามเหลี่ยมระหว่างด้านหน้าของมุมและด้านข้าง y / x

การเปรียบเทียบตรีโกณมิติ tan sin cos ทั้งหมดถูก จำกัด ให้ใช้ได้เฉพาะกับสามเหลี่ยมมุมฉากหรือสามเหลี่ยมมุมฉากที่มีมุม 90 องศาหนึ่งมุมเท่านั้น

ตารางตรีโกณมิติกำลังสองมุมพิเศษ I (0 - 90 องศา)

มุม	0 º	30 º	45วินาที	60 º	90 º
บาป	0	1/2	1/2 √2	1/2 √3	1
คอส	1	1/2 √3	1/2 √2	1/2	0
ตาล	0	1/2 √3	1	√3	∞

ตารางตรีโกณมิติกำลังสองมุมพิเศษ (90 - 180 องศา)

มุม	90 º	120 º	135 º	150 º	180 º
บาป	1	1/2 √3	1/2 √2	1/2	0
คอส	0	- 1/2	- 1/2 √2	- 1/2 √3	-1
ตาล	∞	-√3	-1	- 1/3 √3	0

Sin Cos Tan Table Special Angle Quadrant III (180-270 องศา)

มุม	180 º	210 º	225 º	240 º	270 º
บาป	0	- 1/2	- 1/2 √2	- 1 / 2√3	-1
คอส	-1	- 1 / 2√3	- 1 / 2√2	- 1/2	0
ตาล	0	1 / 3√3	1	√3	∞

ตาราง Cos Sin Tan มุมพิเศษ Quadrant IV (270-360 องศา)

มุม	270 º	300 º	315 º	330 º	360 º
บาป	-1	-½√3	-½√2	-½	0
คอส	0	½	½√2	½√3	1
ตาล	∞	-√3	-1	-1 / 3√3	0

ดังนั้นรายการตารางตรีโกณมิติทั้งหมดจากมุมพิเศษทั้งหมดตั้งแต่ 0-360 องศา

อ่านเพิ่มเติม: กระบวนการกลไกการมองเห็นของมนุษย์และคำแนะนำในการดูแลดวงตา

คุณสามารถใช้ตารางนี้เพื่ออำนวยความสะดวกทางธุรกิจในการคำนวณหรือวิเคราะห์ตรีโกณมิติในคณิตศาสตร์

การเรียกคืนตารางตรีโกณมิติมุมพิเศษโดยไม่ต้องท่องจำ

ในความเป็นจริงคุณไม่ต้องกังวลกับการจำค่าตรีโกณมิติทั้งหมดจากทุกมุม

สิ่งที่คุณต้องมีคือแนวคิดความเข้าใจพื้นฐานที่คุณสามารถใช้เพื่อหาค่าตรีโกณมิติของมุมใดมุมหนึ่ง

คุณต้องจำส่วนประกอบความยาวด้านข้างของสามเหลี่ยมที่มุมพิเศษ 0, 30, 45, 60 และ 90 องศา

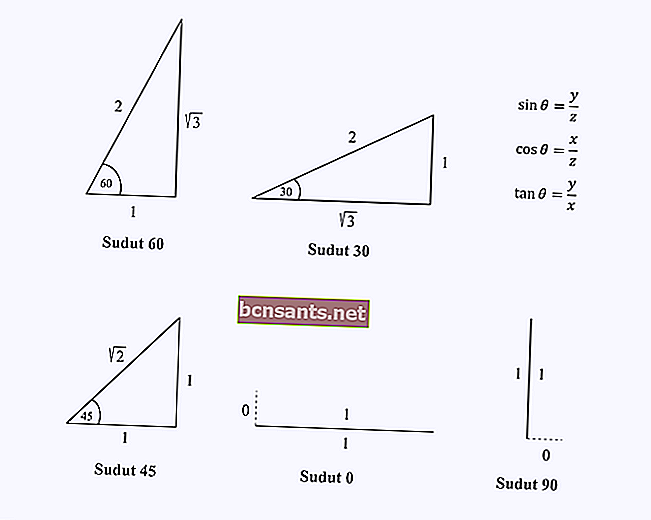
สมมติว่าคุณต้องการหาค่า cos (60)

คุณต้องจำความยาวด้านข้างของสามเหลี่ยมด้วยมุม 60 องศาจากนั้นดำเนินการโคไซน์ซึ่งก็คือ x / z บนสามเหลี่ยมนั้น

จากรูปจะเห็นว่าค่า cos 60 = 1/2

ง่ายใช่มั้ย?

สำหรับมุมในรูปสี่เหลี่ยมอื่น ๆ วิธีการนั้นเหมือนกันและคุณจะต้องปรับเครื่องหมายบวกหรือลบของแต่ละควอดแรนต์

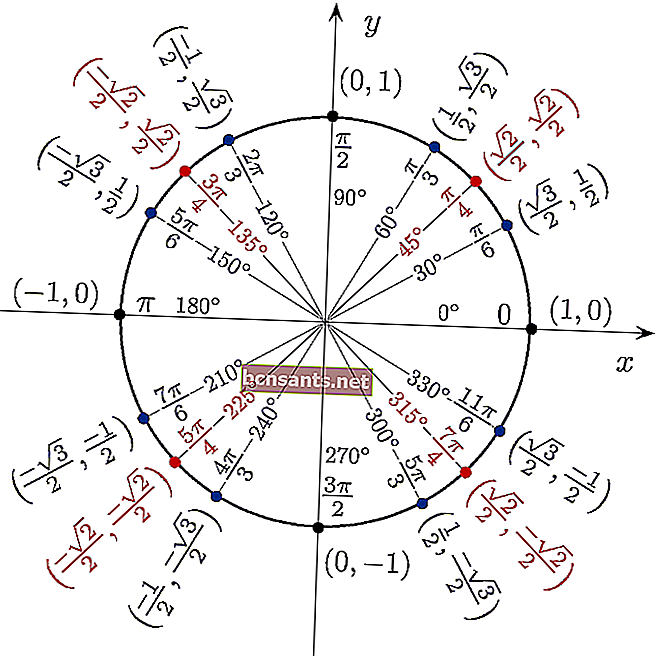
ตารางในรูปวงกลม

หากตาราง cos sin tan ด้านบนยาวเกินไปที่จะจำได้เช่นกันหากวิธีคิดมุมพิเศษที่คุณคิดว่ายังยาก ...

คุณสามารถใช้ตารางตรีโกณมิติในรูปของวงกลมเพื่อดูค่าของ sin cos tan ได้โดยตรงจากมุม 360 องศา

เคล็ดลับง่ายๆในการจดจำตารางตรีโกณมิติ

นอกเหนือจากวิธีการข้างต้นแล้วยังมีอีกหนึ่งวิธีที่คุณสามารถใช้เพื่อจดจำตารางสูตรตรีโกณมิติได้อย่างง่ายดาย

ขั้นตอนที่คุณต้องทำมีดังนี้:

• ขั้นตอนที่ 1 . สร้างตารางที่มีมุม 0 - 90 องศาและคอลัมน์พร้อมคำอธิบาย sin cos tan
• ขั้นตอนที่ 2 . สังเกตว่าสูตรทั่วไปสำหรับบาปที่มุม 0 - 90 องศาคือ√x / 2
• ขั้นตอนที่ 3 . เปลี่ยนค่า x เป็น 0 บน√x / 2 ในคอลัมน์แรก มุมบนซ้าย
• ขั้นตอนที่ 4.กรอกลำดับโดยเปลี่ยน x เป็น 0, 1, 2, 3, 4 ในคอลัมน์ sin ดังนั้นคุณจึงได้ค่าบาปของค่าตรีโกณมิติที่สมบูรณ์
• ขั้นตอนที่ 5 . ในการหาค่า cos สิ่งที่คุณต้องทำคือกลับลำดับในคอลัมน์ sin
• ขั้นตอนที่ 6 . ในการหาค่าของผิวสีแทนสิ่งที่คุณต้องทำคือหารค่าบาปด้วยค่า cos

อ่านเพิ่มเติม: เรื่องแต่ง: ตัวอย่างคำจำกัดความและองค์ประกอบ [FULL

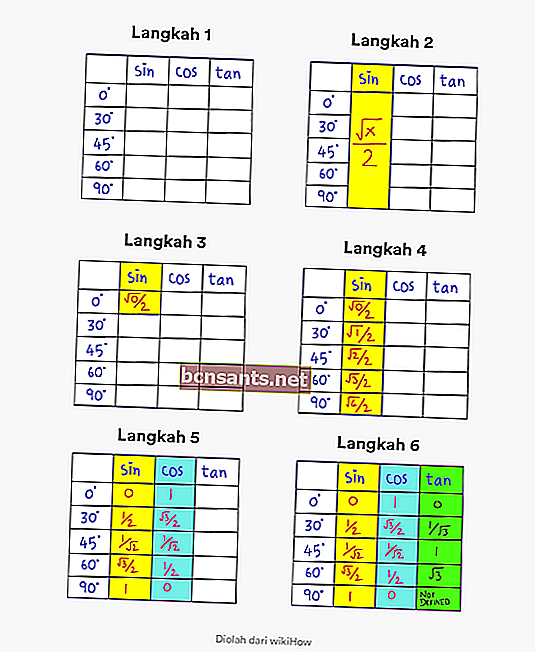
ข้อใดง่ายกว่าที่คุณจะเข้าใจในการจำค่าตรีโกณมิติของ tan sin cos

ไม่ว่าจะด้วยวิธีใดให้เลือกวิธีที่เข้าใจง่ายที่สุด เพราะแต่ละคนมีสไตล์การเรียนรู้ที่แตกต่างกัน.

ตารางสำหรับทุกมุม

หากในตารางด้านบนค่าที่แสดงเป็นเพียงค่าตรีโกณมิติของมุมพิเศษตารางนี้จะแสดงค่าตรีโกณมิติทั้งหมดของมุมทั้งหมดตั้งแต่ 0 - 90 องศา

มุม	เรเดียน	บาป	คอส	ตาล
0 °	0	0	1	0
1 °	0.01746	0.01746	0.99985	0.01746
2 °	0.03492	0.03491	0.99939	0.03494
3 °	0.05238	0.05236	0.99863	0.05243
4 °	0.06984	0.06979	0.99756	0.06996
5 °	0.0873	0.08719	0.99619	0.08752
6 °	0.10476	0.10457	0.99452	0.10515
7 °	0.12222	0.12192	0.99254	0.12283
8 °	0.13968	0.13923	0.99026	0.1406
9 °	0.15714	0.1565	0.98768	0.15845
10 °	0.1746	0.17372	0.9848	0.1764
11 °	0.19206	0.19089	0.98161	0.19446
12 °	0.20952	0.20799	0.97813	0.21265
13 °	0.22698	0.22504	0.97435	0.23096
14 °	0.24444	0.24202	0.97027	0.24943
15 °	0.26191	0.25892	0.9659	0.26806
16 °	0.27937	0.27575	0.96123	0.28687
17 °	0.29683	0.29249	0.95627	0.30586
18 °	0.31429	0.30914	0.95102	0.32506
19 °	0.33175	0.32569	0.94548	0.34448
20 °	0.34921	0.34215	0.93965	0.36413
21 °	0.36667	0.35851	0.93353	0.38403
22 °	0.38413	0.37475	0.92713	0.40421
23 °	0.40159	0.39088	0.92044	0.42467
24 °	0.41905	0.40689	0.91348	0.44543
25 °	0.43651	0.42278	0.90623	0.46652
26 °	0.45397	0.43854	0.89871	0.48796
27 °	0.47143	0.45416	0.89092	0.50976
28 °	0.48889	0.46965	0.88286	0.53196
29 °	0.50635	0.48499	0.87452	0.55458
30 °	0.52381	0.50018	0.86592	0.57763
31 °	0.54127	0.51523	0.85706	0.60116
32 °	0.55873	0.53011	0.84793	0.62518
33 °	0.57619	0.54483	0.83854	0.64974
34 °	0.59365	0.55939	0.8289	0.67486
35 °	0.61111	0.57378	0.81901	0.70057
36 °	0.62857	0.58799	0.80887	0.72693
37 °	0.64603	0.60202	0.79848	0.75396
38 °	0.66349	0.61587	0.78785	0.78172
39 °	0.68095	0.62953	0.77697	0.81024
40 °	0.69841	0.643	0.76586	0.83958
41 °	0.71587	0.65628	0.75452	0.86979
42 °	0.73333	0.66935	0.74295	0.90094
43 °	0.75079	0.68222	0.73115	0.93308
44 °	0.76825	0.69488	0.71913	0.96629
45 °	0.78571	0.70733	0.70688	1,00063
46 °	0.80318	0.71956	0.69443	1.0362
47 °	0.82064	0.73158	0.68176	1.07308
48 °	0.8381	0.74337	0.66888	1.11137
49 °	0.85556	0.75494	0.6558	1.15117
50 °	0.87302	0.76627	0.64252	1. พ.ศ. 2469
51 °	0.89048	0.77737	0.62904	1,2358
52 °	0.90794	0.78824	0.61537	1.28091
53 °	0.9254	0.79886	0.60152	1.32807
54 °	0.94286	0.80924	0.58748	1.37748
55 °	0.96032	0.81937	0.57326	1.42932
56 °	0.97778	0.82926	0.55887	1.48382
57 °	0.99524	0.83889	0.5443	1.54122
58 °	1.0127	0.84826	0.52957	1.60179
59 °	1.03016	0.85738	0.51468	1.66584
60 °	1.04762	0.86624	0.49964	1,73374
61 °	1.06508	0.87483	0.48444	1.80587
62 °	1.08254	0.88315	0.46909	1.8827
63 °	1.1	0.89121	0.4536	1,96476
64 °	1.11746	0.89899	0.43797	2.05265
65 °	1.13492	0.9065	0.4222	2.14707
66 °	1.15238	0.91373	0.40631	2.24884
67 °	1.16984	0.92069	0.3903	2.35894
68 °	1.1873	0.92736	0.37416	2.4785
69 °	1.20476	0.93375	0.35792	2.60887
70 °	1.22222	0.93986	0.34156	2.75169
71 °	1.23968	0.94568	0.3251	2.90892
72 °	1.25714	0.95121	0.30854	3.08299
73 °	1.2746	0.95646	0.29188	3.27686
74 °	1.29206	0.96141	0.27514	3,49427
75 °	1.30952	0.96606	0.25831	3.73993
76 °	1.32698	0.97043	0.2414	4.01992
77 °	1.34444	0.97449	0.22442	4.34219
78 °	1.36191	0.97826	0.20738	4,71734
79 °	1.37937	0.98173	0.19026	5.15984
80 °	1.39683	0.98491	0.1731	5.68998
81 °	1.41429	0.98778	0.15587	6.33709
82 °	1.43175	0.99035	0.1386	7.14523
83 °	1.44921	0.99262	0.12129	8.18379
84 °	1.46667	0.99458	0.10394	9,56868
85 °	1.48413	0.99625	0.08656	11,5092
86 °	1.50159	0.99761	0.06915	14,4259
87 °	1.51905	0.99866	0.05173	19,3069
88 °	1.53651	0.99941	0.03428	29,153
89 °	1.55397	0.99986	0.01683	59.4189
90 °	1.57143	1	0	∞

หวังว่าคำอธิบายตรีโกณมิตินี้จะเป็นประโยชน์กับคุณ

เนื้อหานี้จะเป็นประโยชน์อย่างยิ่งสำหรับการใช้งานต่างๆในคณิตศาสตร์และฟิสิกส์ขั้นสูง

คุณยังสามารถเรียนรู้สื่อการเรียนการสอนอื่น ๆ ได้ที่ Saintif เช่นจำนวนเฉพาะการแปลงหน่วยสูตรสี่เหลี่ยมและอื่น ๆ

ข้อมูลอ้างอิง

• ตรีโกณมิติ - Wikipedia
• เครื่องมือทางคณิตศาสตร์ - ตรีโกณมิติ