
สูตรพีทาโกรัสเป็นสูตรที่ใช้หาความยาวด้านข้างของรูปสามเหลี่ยม
สูตรพีทาโกรัสหรือที่เรียกว่าทฤษฎีบทพีทาโกรัสเป็นหนึ่งในเนื้อหาวิชาคณิตศาสตร์ที่สอนเร็วที่สุด
ตั้งแต่ชั้นประถมเราได้รับการสอนสูตรพีทาโกรัสนี้
ในบทความนี้ฉันจะพูดถึงเรื่องของทฤษฎีบทพีทาโกรัสอีกครั้งพร้อมกับตัวอย่างปัญหาและแนวทางแก้ไข
ประวัติ Pythagoras - Pythagoras
ในความเป็นจริง Pythagoras เป็นชื่อของบุคคลในสมัยกรีกโบราณใน 570 - 495 ปีก่อนคริสตกาล
พีธากอรัสเป็นนักปรัชญาและนักคณิตศาสตร์ที่เก่งกาจในสมัยของเขา นี่เป็นหลักฐานจากการค้นพบของเขาซึ่งประสบความสำเร็จในการแก้ปัญหาความยาวด้านข้างของสามเหลี่ยมด้วยสูตรง่ายๆ
ทฤษฎีบทของพีทาโกรัส
ทฤษฎีบทพีทาโกรัสเป็นประพจน์ทางคณิตศาสตร์เกี่ยวกับรูปสามเหลี่ยมมุมฉากซึ่งแสดงให้เห็นว่าความยาวของฐานของรูปสี่เหลี่ยมจัตุรัสบวกกับความยาวของความสูงของสี่เหลี่ยมเท่ากับความยาวของด้านตรงข้ามมุมฉากของกำลังสอง
สมมติ….
- ความยาวของฐานของสามเหลี่ยมคือก
- ความยาวของความสูงคือ b
- ความยาวของด้านตรงข้ามมุมฉากคือ c
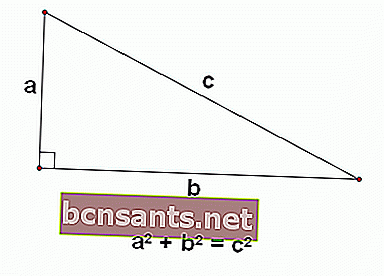
ดังนั้นโดยใช้อาร์กิวเมนต์ของ Pytaghoras ความสัมพันธ์ระหว่างทั้งสามสามารถกำหนดให้เป็นได้
ก2 + ข2 = ค2
การพิสูจน์ทฤษฎีบทพีทาโกรัส
หากคุณเป็นคนช่างสังเกตคุณจะสามารถจินตนาการได้ว่าโดยพื้นฐานแล้วสูตร pytaghoras แสดงให้เห็นว่าพื้นที่ของสี่เหลี่ยมที่มีด้านบวกพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้าน b เท่ากับพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้าน c
คุณสามารถดูภาพประกอบในภาพต่อไปนี้:

คุณสามารถดูได้ในวิดีโอดังต่อไปนี้
วิธีใช้สูตรพีทาโกรัส
phytagoras สูตรa 2 + b 2 = c 2โดยทั่วไปสามารถแสดงได้หลายรูปแบบ ได้แก่ :
a2 + b2 = c2
c2 = a 2 + b 2
a2 = c2 - ข 2
b2 = c2 -a2
ในการแก้ปัญหาแต่ละสูตรเหล่านี้คุณสามารถใช้ค่ารูทของสูตรพีทาโกรัสด้านบน
อ่านเพิ่มเติม: กล้องจุลทรรศน์: คำอธิบายชิ้นส่วนและหน้าที่ของมัน
หมายเหตุสำคัญ:อย่าลืมว่าสูตรข้างต้นใช้กับสามเหลี่ยมด้านขวาเท่านั้น ถ้าไม่เช่นนั้นไม่ถูกต้อง
Triple Pythagoras (รูปแบบตัวเลข)
Pythagorean triple เป็นชื่อของรูปแบบตัวเลข abc ที่ตรงตามสูตรของ Pythagorean ด้านบน
มีตัวเลขมากมายที่เติมเต็ม pytaghoras สามตัวนี้แม้กระทั่งจำนวนมาก
ตัวอย่างบางส่วน ได้แก่ :
- 3 - 4 - 5
- 5 - 12 - 13
- 6 - 8 - 10
- 7 - 24 - 25
- 8 - 15 - 17
- 9 - 12 - 15
- 10 - 24 - 26
- 12 - 16 - 20
- 14 - 48 - 50
- 15 - 20 - 25
- 15 - 36 - 39
- 16 - 30 - 34
- 17 - 144 - 145
- 19 - 180 - 181
- 20 - 21 - 29
- 20 - 99 - 101
- 21 - 220 - 221
- 23 - 264 - 265
- 24–143 - 145
- 25 - 312 - 313
- ฯลฯ
รายการยังคงสามารถดำเนินการต่อไปได้เป็นจำนวนมาก
โดยพื้นฐานแล้วตัวเลขจะตรงกันเมื่อคุณใส่ค่าลงในสูตรa 2 + b 2 = c 2
ตัวอย่างคำถามและการอภิปรายที่สมบูรณ์
เพื่อให้เข้าใจหัวข้อของสูตร Pytaghoras นี้ได้ดีขึ้นลองดูตัวอย่างของคำถามทั้งหมดและการสนทนาด้านล่าง
ตัวอย่างพีทาโกรัสสูตร 1
1. สามเหลี่ยมมีด้าน BC ยาว 6 ซม. และด้าน AC 8 ซม . ด้านตรงข้ามมุมฉาก (AB) เท่ากับกี่ซม.?
การตั้งถิ่นฐาน:
เป็นที่รู้จัก:
- BC = 6 ซม
- AC = 8 ซม
ต้องการ:ความยาว AB?
ตอบ:
AB2 = BC2 + AC2
= 62 + 82
= 36 + 64
= 100
AB = √100
= 10
ดังนั้นความยาวของด้าน AB (เอียง) คือ 10 ซม.
ตัวอย่างทฤษฎีบทพีทาโกรัส 2
2. เป็นที่ทราบกันดีว่าสามเหลี่ยมมีด้านตรงข้ามมุมฉาก ยาว 25 ซม.และด้านแนวตั้งของสามเหลี่ยมมีความยาว 20 ซม . ความยาวของด้านแบนคืออะไร?
การตั้งถิ่นฐาน:
เป็นที่รู้กัน:เราทำตัวอย่างเพื่อให้ง่ายขึ้น
- c = ด้านตรงข้ามมุมฉาก b = ด้านแบน a = ด้านแนวตั้ง
- c = 25 ซม., a = 20 ซม
ต้องการ:ความยาวของด้านแบน (b)?
ตอบ:
b2 = c2 - a2
= 252 - 202
= 625 - 400
= 225
b = √225
= 15 ซม
เพื่อให้ความยาวของด้านแบนของสามเหลี่ยมเท่ากับ 15 ซม .
ตัวอย่างพีทาโกรัสสูตร 3
3. ความยาวของด้านแนวตั้งของสามเหลี่ยมคือเท่าใดถ้าคุณรู้ว่าด้านตรงข้ามมุมฉากของสามเหลี่ยมคือ 20 ซม.และด้านแบนมีความยาว 16 ซม .
วิธีแก้ไข :
เป็นที่รู้จัก:ก่อนอื่นเราสร้างตัวอย่างและค่า
- c = ด้านตรงข้ามมุมฉาก b = ด้านแบน a = ด้านแนวตั้ง
- c = 20 ซม. , b = 16 ซม
ต้องการ:ความยาวของแนวตั้ง (a)?
ตอบ:
a2 = c2 - b2
= 202 - 162
= 400 - 256
= 144
a = √144
= 12 ซม
จากนี้เราจะได้ความยาวของด้านข้างของสามเหลี่ยมที่ตั้งตรงคือ 12 ซม .
ตัวอย่างโจทย์ Triple Pythagoras 4
ต่อค่าของ Pythagorean triple ต่อไปนี้….
3, 4, ….
6, 8, ….
5, 12, ….
การตั้งถิ่นฐาน:
เช่นเดียวกับวิธีแก้ปัญหาในปัญหาก่อนหน้านี้ความสัมพันธ์สามพีทาโกรัสนี้สามารถแก้ไขได้โดยใช้สูตร c2 = a 2 + b 2
ลองคำนวณดูเองครับ….
คำตอบ (ที่จะจับคู่) คือ:
- 5
- 10
- 13
ตัวอย่างโจทย์สูตรพีทาโกรัส 5
กำหนดให้สามเมือง (A, B, C) เป็นรูปสามเหลี่ยมโดยมีข้อศอกอยู่ในเมือง B
ระยะทางถึงเมือง AB = 6 กม., ระยะทางถึงเมือง BC = 8 กม., ระยะทางไปเมือง AC คืออะไร?
การตั้งถิ่นฐาน:
คุณสามารถใช้สูตรทฤษฎีบทพีทาโกรัสและรับผลลัพธ์ของการคำนวณระยะทางของเมือง AC = 10 กม.
ดังนั้นการอภิปรายเกี่ยวกับสูตรพีทาโกรัส - ข้อโต้แย้งของทฤษฎีบทพีทาโกรัสซึ่งนำเสนออย่างเรียบง่าย หวังว่าคุณจะเข้าใจได้ดีเพื่อที่ในภายหลังคุณจะสามารถเข้าใจหัวข้อทางคณิตศาสตร์อื่น ๆ เช่นตรีโกณมิติลอการิทึมและอื่น ๆ
หากคุณยังคงมีคำถามคุณสามารถส่งคำถามได้โดยตรงในคอลัมน์ความคิดเห็น
ข้อมูลอ้างอิง
- โจทย์ของพีธากอรัสคืออะไร? - ขอลูกชาย
- ทฤษฎีบทพีทาโกรัส - คณิตศาสตร์เป็นเรื่องสนุก
