ฟังก์ชันองค์ประกอบ: แนวคิดพื้นฐานสูตรและตัวอย่าง

ฟังก์ชันองค์ประกอบคือการรวมกันของการทำงานของฟังก์ชันสองประเภท f (x) และ g (x) เพื่อให้สามารถสร้างฟังก์ชันใหม่ได้

สูตรฟังก์ชันองค์ประกอบ

สัญลักษณ์ของการทำงานของฟังก์ชั่นการจัดองค์ประกอบเป็น "o" จากนั้นจึงสามารถอ่านองค์ประกอบหรือวงกลม ฟังก์ชันใหม่นี้สามารถสร้างขึ้นจาก f (x) และ g (x) ได้แก่ :

1. (หมอก) (x) ซึ่งหมายความว่า g ถูกป้อนเข้าใน f
2. (gof) (x) ซึ่งหมายความว่า f ใส่เข้าไปใน g

ในฟังก์ชันองค์ประกอบเรียกอีกอย่างว่าฟังก์ชันเดียว

ฟังก์ชั่นเดียวคืออะไร?

ฟังก์ชันเดี่ยวคือฟังก์ชันที่สามารถแสดงด้วยตัวอักษร "หมอก" หรืออ่านได้ว่า "f วงเวียน g" ฟังก์ชัน "หมอก" คือฟังก์ชัน g ซึ่งทำก่อนแล้วตามด้วย f

ในขณะเดียวกันฟังก์ชัน“ gof” จะอ่านฟังก์ชัน g วงเวียน f ดังนั้น "gof" จึงเป็นฟังก์ชันที่ f เสร็จก่อนแทนที่จะเป็น g

จากนั้นฟังก์ชัน (หมอก) (x) = f (g (x)) →ฟังก์ชัน g (x) ประกอบเป็นฟังก์ชัน f (x)

เพื่อให้เข้าใจฟังก์ชันนี้ให้พิจารณาภาพด้านล่าง:

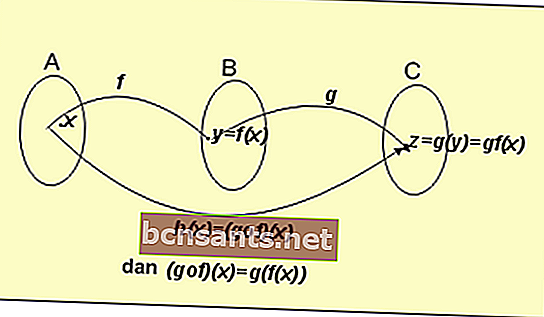
จากรูปแบบสูตรด้านบนคำจำกัดความที่เราได้รับคือ:

ถ้าf: A → B ถูกกำหนดโดยสูตรy = f (x)

ถ้าg: B → C ถูกกำหนดโดยสูตรy = g (x)

จากนั้นเราจะได้ผลลัพธ์ของฟังก์ชัน g และ f:

h (x) = (gof) (x) = g (f (x))

จากคำจำกัดความข้างต้นเราสามารถสรุปได้ว่าฟังก์ชันที่เกี่ยวข้องกับฟังก์ชัน f และ g สามารถเขียนได้:

• (gof) (x) = g (f (x))
• (หมอก) (x) = f (g (x))

คุณสมบัติของฟังก์ชัน Composition

มีคุณสมบัติหลายประการในฟังก์ชันองค์ประกอบซึ่งอธิบายไว้ด้านล่าง

ถ้า f: A → B, g: B → C, h: C → D แล้ว:

1. (หมอก) (x) ≠ (gof) (x) ไม่ใช้ลักษณะการสับเปลี่ยน
2. [fo (goh) (x)] = [(หมอก) oh (x)] เป็นความเชื่อมโยง
3. ถ้าฟังก์ชันเอกลักษณ์คือ I (x) ดังนั้น (fol) (x) = (lof) (x) = f (x)

อ่านเพิ่มเติม: 100+ คำสำหรับเพื่อน (ล่าสุด) ที่สัมผัสหัวใจ

ตัวอย่างปัญหา

ปัญหา 1

กำหนดให้สองฟังก์ชันแต่ละf (x) และg (x) ตามลำดับ ได้แก่ :

f (x) = 3x + 2

ก. (x) = 2 - x

กำหนด:

ก) ( f o g ) (x)

ข) ( g o f ) (x)

ตอบ

เป็นที่รู้จัก:

f (x) = 3x + 2

ก. (x) = 2 - x

( f o g ) (x)

"เสียบg (x) เข้ากับf (x)"

เป็น:

( f o g ) (x) = f ( ก (x))

= f (2 - x)

= 3 (2 - x) + 2

= 6 - 3x + 2

= - 3x + 8

( g o f ) (x)

"เสียบf (x) เข้ากับg (x)"

จนกว่าจะกลายเป็น:

( f o g ) (x) = g ( f (x))

= กรัม (3x + 2)

= 2 - (3x + 2)

= 2 - 3x - 2

= - 3x

ปัญหา 2

หากทราบว่า f (x) = 3x + 4 และ g (x) = 3x ค่าของ (หมอก) (2) คืออะไร

ตอบ:

(หมอก) (x) = f (g (x))

= 3 (3x) + 4

= 9x + 4

(หมอก) (2) = 9 (2) + 4

= 22

ปัญหา 3

ให้ฟังก์ชันf (x) = 3x - 1 และg (x) = 2 × 2 + 3 ค่าขององค์ประกอบของฟังก์ชัน ( g o f ) (1) = ….?

ตอบ

เป็นที่รู้จัก:

f (x) = 3x - 1 และg (x) = 2 × 2 + 3

( ก o ฉ ) (1) = …?

เสียบ f (x) เข้ากับ g (x) แล้วเติมด้วย 1

( g o f ) (x) = 2 (3 x - 1) 2 + 3

( g o f ) (x) = 2 (9 x 2 - 6x + 1) + 3

( g o f ) (x) = 18x 2 - 12x + 2 + 3

( g o f ) (x) = 18 × 2 - 12x + 5

( g o f ) (1) = 18 (1) 2 - 12 (1) + 5 = 11

ปัญหา 4

มีสองฟังก์ชั่น:

f (x) = 2x - 3

ก (x) = x2 + 2x + 3

ถ้า (หมอก) (a) เป็น 33 ให้หาค่า 5a

ตอบ:

ค้นหาก่อน (หมอก) (x)

(หมอก) (x) เท่ากับ 2 (x2 + 2x + 3) - 3

(หมอก) (x) เท่ากับ 2 × 2 4x + 6 - 3

(หมอก) (x) เท่ากับ 2 × 2 4x + 3

33 เหมือนกับ 2a2 4a + 3

2a2 4a - 30 เท่ากับ 0

a2 + 2a - 15 เท่ากับ 0

อ่านเพิ่มเติม: สูตรทางธุรกิจ: คำอธิบายของเนื้อหาตัวอย่างคำถามและการอภิปราย

ปัจจัย:

(a + 5) (a - 3) เท่ากับ 0

a = - 5 หรือเท่ากับ 3

ถึง

5a = 5 (−5) = −25 หรือ 5a = 5 (3) = 15

ปัญหา 5

ถ้า (หมอก) (x) = x² + 3x + 4 และ g (x) = 4x - 5. ค่า f (3) เป็นเท่าใด?

ตอบ:

(หมอก) (x) เท่ากับx² + 3x + 4

f (g (x)) เท่ากับx² + 3x + 4

g (x) เท่ากับ 3 ดังนั้น

4x - 5 เท่ากับ 3

4x เท่ากับ 8

x เท่ากับ 2

f (g (x)) = x² + 3x + 4 และสำหรับ g (x) เท่ากับ 3 เราจะได้ x เท่ากับ 2

ถึง: f (3) = 2² + 3 2 + 4 = 4 + 6 + 4 = 14

ดังนั้นคำอธิบายเกี่ยวกับสูตรฟังก์ชัน Composition จึงเป็นตัวอย่างของปัญหา อาจมีประโยชน์.