
ความถี่ที่คาดไว้คือจำนวนการปรากฏที่คาดไว้ในเหตุการณ์โดยทำการทดลองซ้ำ ๆ ซึ่งเรียกอีกอย่างว่าการทดลองทดสอบ
หรือผลคูณของโอกาสของเหตุการณ์ตัวอย่างเช่นเหตุการณ์ A ที่มีจำนวนการทดลองที่ดำเนินการ
พูดง่ายๆคือคุณเคยเล่น Ludo หรือไม่? ทอยลูกเต๋าสองลูกในเวลาเดียวกันและคาดว่าจะมีหกลูกปรากฏบนลูกเต๋าทั้งสองลูก? ถ้าเป็นเช่นนั้นก็หมายความว่าคุณได้ประยุกต์ใช้ทฤษฎีของความถี่ที่คาดว่า
สูตรความถี่ที่คาดไว้
โดยทั่วไปสูตรสำหรับความถี่ที่คาดหวังมีดังนี้:
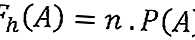
ข้อมูล:
F h (A) = ความถี่ที่คาดหวังของเหตุการณ์ A
n = จำนวนครั้งที่เกิดขึ้น A
P (A) = ความน่าจะเป็นของเหตุการณ์ A
ตัวอย่างคำถามเกี่ยวกับความถี่ที่คาดหวัง
ตัวอย่างปัญหา 1
- ทอยลูกเต๋าสองลูกพร้อมกัน 144 ครั้ง กำหนดโอกาสที่สิ่งที่หวังจะเกิดขึ้น
- ทั้งหกตายทั้งคู่
- จำนวนรวมหกลูกเต๋าทั้งสองลูก
การตั้งถิ่นฐาน:
ในการแก้ปัญหาเช่นนี้ก่อนอื่นให้คำนวณจำนวนเหตุการณ์ทั้งหมด เหตุการณ์ทั้งหมดแสดงโดย S จากนั้น:
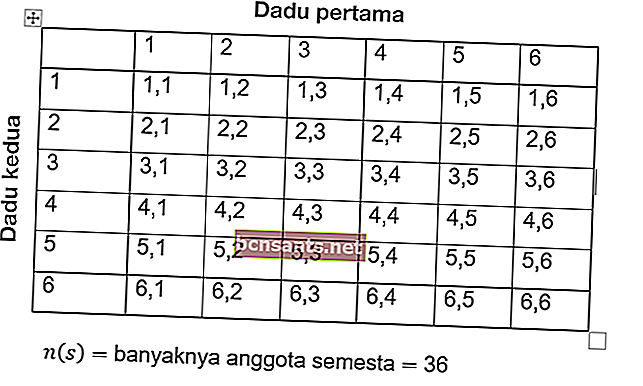
เพื่อให้จำนวนสมาชิกของจักรวาลของตัวเลขคือ n (s) = 36
1. การปรากฏตัวของหมายเลขหกบนลูกเต๋าทั้งสองลูก
สำหรับตัวเลขสองตัวที่ปรากฏเพียงตัวเดียวคือ (6,6) จากนั้น:
n (1) = 1
จากนั้นจำนวนการทดลอง 144 ครั้ง
n = 144
ด้วยประการฉะนี้
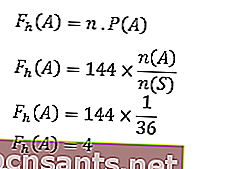
ดังนั้นความถี่ที่คาดว่าจะปรากฏของหมายเลขหกบนลูกเต๋าทั้งสองลูกคือ 4 เท่า
2. ลักษณะของลูกเต๋าจำนวนรวมหก
สำหรับจำนวนลูกเต๋าทั้งหมดหกลูก ได้แก่

จากนั้นจำนวนการทดลอง 144 ครั้ง

ด้วยประการฉะนี้

ดังนั้นความถี่ที่คาดว่าจะปรากฏของลูกเต๋าหกลูกคือ 20 เท่า
ตัวอย่างปัญหา 2
เหรียญหนึ่งที่โยนขึ้นไปในอากาศ 30 ครั้ง กำหนดความถี่ที่คาดว่าจะปรากฏในด้านตัวเลข
อ่านเพิ่มเติม: สูตรการเร่ง + ตัวอย่างปัญหาและแนวทางแก้ไขการตั้งถิ่นฐาน:
จักรวาลของเหตุการณ์นี้มีเพียงสองด้านคือด้านจำนวนและด้านรูปภาพหรือเขียนลงไป

จากนั้น n (S) = 2
จำนวนเหรียญที่โยนคือ 30 ครั้งจากนั้น n = 30
มีเพียงด้านเดียวของจำนวนดังนั้น n (A) = 1
ความถี่ของเหตุการณ์ที่คาดไว้คือ
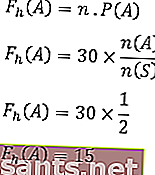
ดังนั้นความถี่ที่คาดว่าจะปรากฏของด้านตัวเลขคือ 20 ครั้ง
สรุป
ดังนั้นความถี่ที่คาดหวังจึงเป็นความถี่หรือจำนวนการทดลองคูณด้วยความน่าจะเป็นของเหตุการณ์ซึ่งทำให้จำนวนความคาดหวังที่ปรากฏในเหตุการณ์หนึ่ง ๆ
หลังจากคำอธิบายข้างต้นคุณสามารถคำนวณความหวังในการถูกลอตเตอรี่ได้หรือไม่? คุณควรใช้กลเม็ดใดเพื่อให้ความหวังในการชนะสูง?
เขียนเคล็ดลับที่แน่นอนของคุณในความคิดเห็นและแจ้งให้พวกเขาทราบ
ดังนั้นคำอธิบายของสูตรและความเข้าใจรวมถึงตัวอย่างความถี่ของความคาดหวังหวังว่านี่จะเป็นประโยชน์และพบกันใหม่ในเนื้อหาต่อไป
