การรวบรวมสูตรคณิตศาสตร์สำหรับ Class 6 SD

ชุดสูตรคณิตศาสตร์สำหรับ SD ชั้นประถมศึกษาปีที่ 6 ต่อไปนี้ประกอบด้วย:

ชุดสูตรปริมาตรสำหรับการสร้างพื้นที่สูตรสำหรับมาตราส่วน
การคำนวณพื้นที่ราบ
การดำเนินการจำนวนเต็ม
สูตรการดำเนินการนับจำนวนผสม
สูตรสำหรับ FPB และ KPK เป็นสองตัวเลข
การประมวลผลและการนำเสนอข้อมูล
สูตรระบบพิกัดปริมาตรและเวลา
การบวกและการลบเศษส่วนและกำหนดค่ารากที่สองของเลขลูกบาศก์

สูตรคณิตศาสตร์ชั้นประถมศึกษาปีที่ 6 คำนวณปริมาณการสร้างห้อง

ชื่อ Build Space	สูตรปริมาตร
หลอด	V = phi r² xt
พรีม่าสามเหลี่ยมตั้งตรง	V = พื้นที่ฐาน x ความสูง

รุ่นที่ 6 คณิตศาสตร์สูตรการเก็บคำนวณชั่ง

สูตรมาตราส่วน	= ระยะทางบนภาพ (แผนที่) / ระยะทางจริง
สูตรระยะทางในรูป	= ระยะทางจริง x มาตราส่วน
สูตรระยะทางจริง	= ระยะทางบนภาพ (แผนที่) / มาตราส่วน

การรวบรวมสูตรเพื่อคำนวณพื้นที่ของแฟลต

รูปสองมิติ	สูตรพื้นที่
สร้าง Flat Square	L = ด้าน x ด้าน = s²
สร้างสามเหลี่ยมแบน	L = ½ฐาน x สูง
สร้าง Flat Circle	L = phi x r²
สร้างรูปสี่เหลี่ยมคางหมู	L = ½เสื้อ× (a + b)
สร้างว่าวแบน - ว่าว	L = ½ xd ₁ xd ₂
สร้าง Flat Parallelogram	L = ฐาน x สูง
ลุกขึ้นแบน Rhombus	L = ½ xd ₁ xd ₂
สร้างสี่เหลี่ยมผืนผ้าแบน	L = ความยาว x กว้าง

การรวบรวมสูตรการดำเนินการจำนวนเต็ม SD คลาส 6

คุณสมบัติการสับเปลี่ยนของการบวกสูตรทั่วไป: a + b = b + a

ตัวอย่างเช่น 2 + 4 = 4 + 2 = 6 หรือ 5 + 10 = 10 + 5 = 15

ลักษณะการสับเปลี่ยนของการคูณสูตรทั่วไป: axb = bxa

ตัวอย่างเช่น 3 x 5 = 5 x 3 = 15 หรือ 10 x 2 = 2 x 10 = 20

คุณสมบัติการกระจายของการคูณกับการบวก

สูตรทั่วไป: ขวาน (b + c) = (axb) + (axc)

ตัวอย่าง:

2 x (5 + 10)	= 2 x 5 + 2 x 10
	= 10 + 20
	= 30

ลักษณะการกระจายของการคูณกับการลบ

สูตรทั่วไป: ขวาน (b - c) = (axb) - (axc)

ตัวอย่าง:

2 x (10 - 5)	= 2 x 10 - 2 x 5
	= 20 + 10
	= 10

การรวบรวมสูตรการคำนวณจำนวนผสม

การดำเนินการคำนวณตัวเลขผสมมี 2 เงื่อนไข ได้แก่ :

อ่านเพิ่มเติม: ลักษณะของดาวเคราะห์ในระบบสุริยะ (เต็ม) พร้อมรูปภาพและคำอธิบาย

ขั้นแรกหากมีวงเล็บ () ให้ทำสิ่งที่อยู่ในวงเล็บก่อน

ประการที่สองถ้าไม่มีวงเล็บ () ให้ทำการคูณ & หารก่อนจากนั้นทำการบวกและลบ

ตัวอย่าง:

= 7000 - 40 x 100: 4 + 200		= 1,000: 10 x 2 - (200 + 50)
= 7000 - 1,000 + 200		= 1,000: 10 x 2 - 150
= 6200	หรือ	= 100 x 2 - 150
		= 200 - 150
		= 50

สูตรสำหรับ FPB และ KPK คือสองตัวเลข

วิธีการกำหนด FPB (ปัจจัยร่วมที่ใหญ่ที่สุด) สำหรับตัวเลขสองตัวและอื่น ๆ ให้ค้นหาปัจจัยในแต่ละตัวเลขเหล่านี้กำหนด Common Factor ของตัวเลขสองตัวและคูณ Common Factor (ตัวประกอบเดียวกัน) ซึ่งมีกำลังน้อยที่สุด

ตัวอย่าง:

27	= 3³
18	= 2 x 3²

ปัจจัยทั่วไปสำหรับ FPB ของเลขสองตัวคือ 3 และกำลังต่ำสุดคือ3² = 9

วิธีการหาค่า LCM (ตัวคูณร่วมน้อยที่สุด) สำหรับตัวเลขสองตัวและอื่น ๆ ให้ค้นหาตัวประกอบเฉพาะของแต่ละตัวเลขเหล่านี้คูณปัจจัยและปัจจัยทั้งหมดที่เหมือนกันอันดับสูงสุดจะถูกเลือก

ตัวอย่างเช่นค่า KPK 12 และ 15

12	= 2² x 3
15	= 3 x 5

ค่า LCM สองตัวเลขด้านบน: 2² x 3 x 5 = 50

การประมวลผลและการนำเสนอข้อมูล

โหมดคือค่าที่ปรากฏมากที่สุด

ค่าต่ำสุดคือค่าที่น้อยที่สุดและต่ำสุดของข้อมูลทั้งหมด

ค่าสูงสุดคือค่าสูงสุดของข้อมูลทั้งหมดในนั้น

ค่าเฉลี่ยคือการหาค่าเฉลี่ยโดยการรวมตัวอย่างทั้งหมดหารด้วยจำนวนตัวอย่าง

การค้นหาระบบพิกัด
แกน x เรียกอีกอย่างว่า Absis (x) และแกน y เรียกอีกอย่างว่า Ordinate (y)
ระนาบพิกัดคาร์ทีเซียนจะประกอบขึ้นด้วย 2 แกนคือแกนตั้งตรง (แกน y) และแกนนอน (แกน x)
จากจุดศูนย์แกนแนวตั้งจะขึ้นและแกนนอนจะอยู่ทางขวาซึ่งมีค่าเป็นบวก
จากจุดศูนย์แกนตั้งตรงจะลงไปและแกนแนวนอนจะไปทางซ้ายซึ่งมีค่าเป็นลบ
การหาพิกัดของวัตถุสามารถหาได้โดยการหาตำแหน่งบนแกน x ทางขวาหรือทางซ้ายโดยให้ตำแหน่งบนแกน y ขึ้นหรือลง

อ่านเพิ่มเติม: คำถามคณิตศาสตร์ระดับ 6 (+ การอภิปราย) SD UASBN - Complete

ความสัมพันธ์ของหน่วยปริมาณ

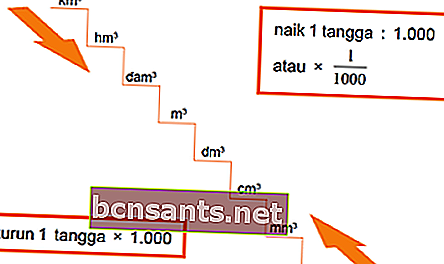
ตัวอย่าง:

1 km3 = 1,000 hm3 (ลง 1 บันได)

1 m3 = 1,000,000 cm3 (ลง 2 บันได)

1 m3 = 1 / 1,000 dam3 (ขึ้น 1 บันได)

1 m3 = 1 / 1,000,000 hm3 (ขึ้น 2 บันได)

ปริมาตรเป็นลิตร

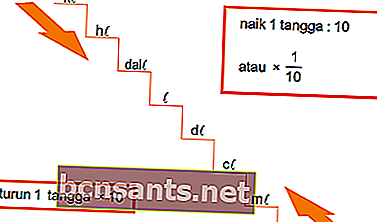
หน่วยเวลา

หนึ่งนาที	= 60 วินาที
หนึ่งชั่วโมง	= 60 นาที
วันหนึ่ง	= 24 ชั่วโมง
หนึ่งอาทิตย์	= 7 วัน
หนึ่งเดือน	= 30 วัน / 31 วัน
หนึ่งเดือน	= 4 สัปดาห์
หนึ่งปี	= 52 สัปดาห์
หนึ่งปี	= 12 เดือน
หนึ่ง Windu	= 8 ปี
หนึ่งทศวรรษ	= 10 ปี
หนึ่งทศวรรษ	= 10 ปี
หนึ่งศตวรรษ	= 100 ปี
หนึ่งมิลเลนเนียม	= 1,000 ปี

การแปลงวินาที

1 นาที = 60 วินาที
1 ชั่วโมง = 3 600
1 วัน = 86 400
1 เดือน = 2,592,000 วินาที
1 ปี = 31104000 วินาที

การบวกและการลบเศษส่วน

เพื่อให้สามารถบวกและลบเศษส่วนได้ก่อนอื่นให้ทำให้ตัวส่วนเท่ากัน

ตัวอย่าง:

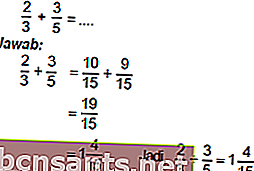
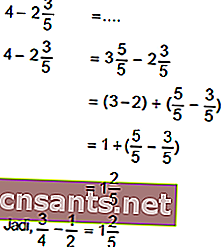
การคูณและการหารเศษส่วน

การคูณเศษส่วนนั้นค่อนข้างง่าย ตัวเศษคูณตัวเศษ ตัวส่วนคูณตัวส่วน หากสามารถทำให้ง่ายขึ้นได้ให้ทำให้ง่ายขึ้น:

การหารเศษส่วนจะเหมือนกับการคูณด้วยตัวหารของเศษส่วน

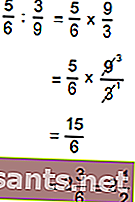
ค้นหารูทลูกบาศก์ของจำนวนลูกบาศก์

13 ถูกอ่านว่ายกกำลังสาม = 1 × 1 × 1 = 1

23 ถูกอ่านเป็นสองยกกำลังสาม = 2 × 2 × 2 = 8

33 ถูกอ่านเป็นสามลูกบาศก์ = 3 × 3 × 3 = 27

43 ถูกอ่านเป็นสี่ยกกำลังสาม = 4 × 4 × 4 = 64

53 ถูกอ่านเป็นห้ายกกำลังสาม = 5 × 5 × 5 = 125

1, 8, 27, 64, 125 และอื่น ๆ คือเลขลูกบาศก์หรือเลขยกกำลัง 3

การบวกและการลบ

23 + 33 = (2 × 2 × 2) + (3 × 3 × 3)

= 8 + 27

= 35

63 - 43 = (6 × 6 × 6) - (4 × 4 × 4)

= 216 - 64

= 152

การคูณและการหาร

23 × 43 = (2 × 2 × 2) × (4 × 4 × 4)

= 8 × 64

= 512

63: 23 = (6 × 6 × 6): (2 × 2 × 2)

= 216: 8

= 27

นั่นคือชุดสูตรคณิตศาสตร์ระดับประถมศึกษาปีที่ 6 ซึ่งมักปรากฏในคำถามการสอบปลายภาคเรียนแห่งชาติ (UAN) และการสอบระดับชาติ (UN) อาจมีประโยชน์.