
อนุกรมเลขคณิตเป็นรูปแบบหมายเลขซีเรียลในคณิตศาสตร์ซึ่งมีประโยชน์ที่สำคัญมากในรูปแบบต่างๆ
ตัวอย่างเช่นเมื่อคุณประหยัดทุกวันคุณทิ้งค่าเผื่อไว้เป็นประจำทุกวันห้าพันรูเปียห์ในวันถัดไปจะเป็นหมื่นและต่อ ๆ ไป เมื่อเวลาผ่านไปเงินของคุณเพิ่มขึ้นใช่ไหม?
รูปแบบการบวกนี้เรียกว่าอนุกรมเลขคณิต
ก่อนที่เราจะพูดถึงลำดับเลขคณิตเราต้องทำความเข้าใจเกี่ยวกับลำดับเลขคณิตก่อนเพราะรูปแบบการบวกที่ได้จากลำดับเลขคณิตมาจากลำดับเลขคณิต
ลำดับเลขคณิต
ลำดับเลขคณิต (Un) คือลำดับของตัวเลขที่มีรูปแบบคงที่ตามการบวกและการลบ
ลำดับเลขคณิตประกอบด้วยเทอมแรก (U 1 ) เทอมที่สอง (U 2 ) และอื่น ๆ มากถึง n หรือเทอมที่ n (Un)
แต่ละเผ่ามีความเหมือนหรือแตกต่างกัน ความแตกต่างระหว่างแต่ละเผ่าคือสิ่งที่เรียกแตกต่างสัญลักษณ์เป็นข ในระยะแรก U 1ยังเป็นสัญลักษณ์เป็น
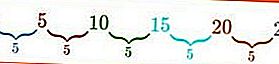
ลำดับเลขคณิต: 0,5,10,15,20,25, …., Un
ตัวอย่างข้างต้นคือลำดับเลขคณิตที่มีความแตกต่างเหมือนกันคือ b = 5 และเทอมแรกคือ a = 0 ความแตกต่างจะได้รับจากการลบแต่ละเผ่า ตัวอย่างเช่นเทอมที่สอง U 2ลบเทอมแรกU 1 , b = U 2 - U 1 = 5 - 0 = 5 ค่าของ b สามารถหาได้จากพจน์ที่สามลบด้วยเทอมที่สองเป็นต้นง่าย ๆ ไม่ใช่หรือ
ตอนนี้ในการค้นหาสูตรของพจน์ที่ n (Un) เราสามารถใช้สูตรที่ใช้ได้จริงที่ใช้งานง่าย

โดยที่Unคือเทอมที่ n, U n-1คือเทอมก่อน n, aคือเทอมแรก, bคือผลต่างและ n เป็นจำนวนเต็ม
สำหรับรายละเอียดเพิ่มเติมเกี่ยวกับวัสดุอนุกรมเลขคณิตให้พิจารณาคำถามตัวอย่างต่อไปนี้
1. ให้ลำดับเลขคณิต 3,7,11,15, …., Un. บรรทัดที่สิบ U 10ด้านบนคืออะไร?
อ่านเพิ่มเติม: 25+ แนะนำภาพยนตร์วิทยาศาสตร์ที่ดีที่สุดตลอดกาล [อัปเดตล่าสุด]อภิปรายผล:
เป็นที่ทราบกันดีจากลำดับข้างต้นว่าเทอมแรกaคือ 3 มีความแตกต่างของbคือ 4 และ n = 10
ยู10เทอมสิบคืออะไร? โดยใช้สูตรก่อนหน้า U 10 จะได้รับดังนี้
U n = a + (n-1) ข
ยู10 = 3 + (10-1) 4
= 3 + 36
= 39
ดังนั้นเทอมที่สิบในลำดับเลขคณิตด้านบนคือ 39
ความก้าวหน้าทางคณิตศาสตร์
ตามที่กล่าวไว้ก่อนหน้าลำดับเลขคณิตระบุลำดับของตัวเลข U 1 , U 2 , ... , U nซึ่งมีรูปแบบเดียวกัน ในขณะเดียวกันลำดับเลขคณิตคือผลรวมของการจัดเรียงตัวเลขในลำดับเลขคณิต U 1 + U 2 + … + Un ถึง n- เทอม
แนวคิดที่แท้จริงสำหรับอนุกรมเลขคณิตนี้เป็นเรื่องง่ายเพราะเราจะเพิ่มลำดับเลขคณิตที่เราพูดถึงก่อนหน้านี้เข้ากับพจน์ที่ n ขึ้นอยู่กับสิ่งที่เรียง
ตัวอย่างเช่นเราเพิ่มลำดับของปัญหาตัวอย่างก่อนหน้านี้ในเทอมที่สี่ง่ายใช่ไหม แต่ถ้าคุณบวกลำดับเลขคณิตเป็นพจน์ที่ 100 ล่ะมันยากขนาดนี้ได้ยังไง
ดังนั้นเพื่อให้ง่ายต่อการคำนวณอนุกรมเลขคณิตนี้จึงใช้สูตรที่ใช้ได้จริง
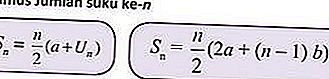
ด้วย
a เป็นเทอมแรก
b แตกต่างกัน
Sn คือจำนวนของพจน์ที่ n
ตัวอย่างโจทย์อนุกรมเลขคณิต
ให้ลำดับเลขคณิต 3 + 7 + 11 + 15 + …. + Un. กำหนดจำนวนเทอมที่สิบ U 10 ในชุดด้านบน
การอภิปราย :
เป็นที่ทราบกันดีว่าในอนุกรมข้างต้น a = 3, b = 4 และ n = 10 จะถูกถามว่าจำนวนพจน์ที่ 10 ในอนุกรมข้างต้นเป็นเท่าใด
โดยใช้สูตร
Sn = n / 2 (2a + (n-1) ข)
S 10 = 10/2 (2.3+ (10-1) 4)
= 5. (6 + 36)
= 210
ดังนั้นจำนวนลำดับของ 10 เทอมข้างต้นคือ 252
คุณเข้าใจเนื้อหาเกี่ยวกับอนุกรมเลขคณิตแล้วเพื่อให้มีความเชี่ยวชาญมากยิ่งขึ้นในการทำงานกับปัญหาอนุกรมโปรดดูตัวอย่างคำถามต่อไปนี้
1. มีลำดับเลขคณิตโดยมี 10 เทอมแรกและเทอมที่ 6 20
ก. กำหนดความแตกต่างของอนุกรมเลขคณิต
ข. เขียนลำดับเลขคณิต
ค. กำหนดผลรวมของหกพจน์แรกของลำดับเลขคณิต
อ่านเพิ่มเติม: แนวคิดหลัก / แนวคิดหลักคือ ... (นิยามประเภทและลักษณะ) เสร็จสมบูรณ์การอภิปราย :
ถ้า a = 10 และ U6 = 20
ก. Un = a + (n-1) ข
U6 = a + (6-1) ข
20 = 10+ (5) ข
b = 10/5 = 2
ข. ลำดับเลขคณิต: 10 + 12 + 14 + 16 + 18 + 20 + … + Un
ค. จำนวน S6 เทอมที่หก
Sn = n / 2 (2a + (n-1) ข)
S6 = 6/2 (2.10+ (6-1) 2)
= 3 (20 + 10)
= 90
ดังนั้นผลรวมของเทอมที่หกในชุดด้านบนคือ 90
2. กำหนดลำดับเลขคณิต: 2, 6, 10, 14, 18, ……… U n . กำหนดสูตรสำหรับพจน์ที่ n ในลำดับเลขคณิต
อภิปรายผล:
ระบุว่าเส้นเลขคณิตด้านบน a = 2 และ b = 4 ถูกถามถึงสูตรสำหรับพจน์ที่ n
Un = a + (n-1) ข
Un = 2+ (n-1) 4
Un = 2 + 4n-4
Un = 4n-2
ดังนั้นสูตรที่ n สำหรับแถวด้านบนคือ Un = 4n-2
นั่นคือเนื้อหาเกี่ยวกับอนุกรมเลขคณิตฉันหวังว่าคุณจะเข้าใจดี!
ข้อมูลอ้างอิง : ลำดับเลขคณิตและผลรวม - คณิตศาสตร์เป็นเรื่องสนุก
