
สูตรสำหรับสามเหลี่ยมเพื่อหาพื้นที่ของรูปทรงคือ 1/2 x ฐาน x สูงเพื่อหาเส้นรอบวงของสามเหลี่ยมซึ่งสามารถหาได้โดยการเพิ่มความยาวของแต่ละด้านของสามเหลี่ยม
ในวิชาคณิตศาสตร์เราได้รับการสอนเกี่ยวกับรูปร่างต่างๆ หนึ่งในนั้นคือรูปทรงสามเหลี่ยม รูปทรงสามเหลี่ยมเป็นรูปทรงที่เรียบง่ายที่สุดในบรรดารูปร่างประเภทต่างๆ
รูปสามเหลี่ยมประกอบด้วยสามด้านโดยมีมุมสามมุมล้อมรอบด้วยส่วน นอกจากนี้มุมรวมของสามเหลี่ยมคือ 180 องศา
สามเหลี่ยมมีหลายประเภท ตามความยาวของด้านข้างมีสามเหลี่ยมด้านเท่าที่มีความยาวด้านเท่ากันสามเหลี่ยมหน้าจั่วที่มีขาสองข้างเท่ากันและสามเหลี่ยมใด ๆ ที่มีความยาวต่างกันสามด้าน
ในขณะเดียวกันจากมุมนั้นมีสามเหลี่ยมมุมฉากที่มีมุมหนึ่งน้อยกว่า 90 องศาสามเหลี่ยมมุมป้านที่มีมุมหนึ่งมากกว่า 90 องศาและสามเหลี่ยมมุมฉากที่มีมุม 90 องศาหนึ่งมุม
เกี่ยวกับรูปสามเหลี่ยมมีส่วนประกอบหลายอย่างที่จำเป็นต้องทราบรวมทั้งพื้นที่และปริมณฑลของสามเหลี่ยม ต่อไปนี้เป็นคำอธิบายเกี่ยวกับพื้นที่และเส้นรอบวงของสามเหลี่ยมพร้อมกับตัวอย่างของปัญหา
พื้นที่ของสามเหลี่ยม

พื้นที่พื้นที่หรือพื้นที่เป็นปริมาณที่แสดงขนาดสองมิติกล่าวคือส่วนหนึ่งของพื้นผิวที่กำหนดไว้อย่างชัดเจนโดยเส้นโค้งหรือเส้นปิด
พื้นที่ของสามเหลี่ยมคือขนาดของสามเหลี่ยมนั่นเอง ต่อไปนี้เป็นสูตรสำหรับพื้นที่ของสามเหลี่ยม:
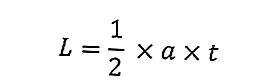
โดยที่ L คือพื้นที่ของสามเหลี่ยม (ซม. 2 ), a คือฐานของสามเหลี่ยม (ซม.) และ h คือความสูงของสามเหลี่ยม (ซม.)
ตัวอย่างพื้นที่ของปัญหาสามเหลี่ยม
ตัวอย่างปัญหา 1
มีสามเหลี่ยมเฉียบพลันที่มีความยาวฐาน a = 10 ซม. และมีความสูง h = 8 ซม. คำนวณพื้นที่ของสามเหลี่ยม
อ่านเพิ่มเติม: สัตว์: ลักษณะประเภทตัวอย่าง [คำอธิบายแบบเต็ม]วิธีการแก้:
ถ้า: a = 10 ซม., h = 8 ซม
ต้องการ: พื้นที่ของสามเหลี่ยม?
ตอบ:
L = ½ xaxt
= ½ x 10 x 8
= 40 ซม. 2
ดังนั้นพื้นที่ของสามเหลี่ยมเฉียบพลันคือ40 ซม. 2
ตัวอย่างปัญหา 2
สามเหลี่ยมมุมฉากมีฐาน 15 ซม. และสูง 20 ซม. ค้นหาและคำนวณพื้นที่ของสามเหลี่ยมมุมฉาก
วิธีการแก้:
ถ้า: a = 15 ซม., h = 20 ซม
ต้องการ: พื้นที่ของสามเหลี่ยม?
ตอบ:
L = ½ xaxt
= ½ x 15 x 20
= 150 ซม. 2
ดังนั้นพื้นที่ของสามเหลี่ยมมุมฉากคือ150 ซม. ²
ตัวอย่างปัญหา 3
สามเหลี่ยมป้านที่มีฐาน 8 ซม. และสูง 3 ซม. แล้วพื้นที่ของสามเหลี่ยมคืออะไร?
วิธีการแก้:
ถ้า: a = 8 cm, h = 3 cm
ต้องการ: พื้นที่ของสามเหลี่ยม?
ตอบ:
L = ½ xaxt
= ½ x 8 x 3
= 12 ซม. 2
ดังนั้นพื้นที่ของสามเหลี่ยมป้านคือ12 ซม. 2
ตัวอย่างปัญหา 4
สามเหลี่ยมหน้าจั่วที่มีความยาวด้านเดียวกันคือ 13 ซม. และฐานของสามเหลี่ยมเท่ากับ 10 ซม. พื้นที่ของสามเหลี่ยมหน้าจั่วคืออะไร?
วิธีการแก้:
คุณรู้ว่า: s = 13 cm, a = 10 cm
ต้องการ: พื้นที่ของสามเหลี่ยม?
ตอบ:
ไม่ทราบความสูงของสามเหลี่ยมดังนั้นเราจึงใช้สูตรพีทาโกรัสเพื่อหาความสูงของสามเหลี่ยม:

เนื่องจากทราบความสูงของสามเหลี่ยมแล้ว:
L = ½ xaxt
= ½ x 10 x 12
= 60 ซม. 2
ดังนั้นพื้นที่ของสามเหลี่ยมหน้าจั่วคือ60 ซม. 2
ปริมณฑลของสามเหลี่ยม

เส้นรอบรูปคือจำนวนด้านในรูปทรงสองมิติ ดังนั้นเส้นรอบวงของสามเหลี่ยมก็คือผลรวมของด้านข้างของสามเหลี่ยมนั่นเอง
นี่คือสูตรสำหรับเส้นรอบวงของสามเหลี่ยม:
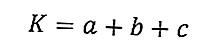
โดยที่ K คือเส้นรอบวงของสามเหลี่ยม (ซม.) และ a, b, c คือความยาวด้านข้างของสามเหลี่ยม (ซม.)
ตัวอย่างปริมณฑลของสามเหลี่ยม
ตัวอย่างปัญหา 1
สามเหลี่ยมด้านเท่ามีด้านยาว 15 ซม. เส้นรอบวงของสามเหลี่ยมคืออะไร?
วิธีการแก้:
คุณรู้ไหมว่าความยาวด้าน = 15 ซม
ถามว่า เส้นรอบวง = ….?
ตอบ:
K = ด้าน a + ด้าน b + ด้าน c
เนื่องจากเป็นรูปสามเหลี่ยมด้านเท่าความยาวของด้านทั้งสามจึงเท่ากัน
K = 15 + 15 + 15
= 45 ซม
ดังนั้นใน ปริมณฑลของรูปสามเหลี่ยมด้านเท่าเป็น45 ซม.
อ่านเพิ่มเติม: การโต้ตอบทางสังคมคือ - คำจำกัดความและคำอธิบายที่สมบูรณ์ตัวอย่างปัญหา 2
สามเหลี่ยมตามอำเภอใจมีด้าน 3 ซม. 5 ซม. และ 8 ซม. คำนวณเส้นรอบวงของสามเหลี่ยม
วิธีการแก้:
คุณรู้ว่า: a = 3 ซม., b = 5 ซม. และ c = 8 ซม
ถามว่าเส้นรอบวง = ….?
ตอบ:
K = ด้าน a + ด้าน b + ด้าน c
= 3 + 5 + 8
= 16 ซม
ดังนั้น เส้นรอบวงของสามเหลี่ยมคือ 16 ซม
ตัวอย่างปัญหา 3
สามเหลี่ยมหน้าจั่วมีด้านเท่ากับ 10 ซม. และฐาน 6 ซม. คำนวณเส้นรอบวงของสามเหลี่ยมหน้าจั่ว
วิธีการแก้:
คุณรู้ไหม: ด้านข้างยาว 10 ซม. และยาว 6 ซม
ถามว่า เส้นรอบวง = ….?
ตอบ:
K = ด้าน a + ด้าน b + ด้าน c
เนื่องจากรูปสามเหลี่ยมเป็นหน้าจั่วจึงมีสองด้านที่มีความยาวเท่ากันคือ 10 ซม. จากนั้น K = 10 + 10 + 6 = 26 ซม.
ดังนั้นเส้นรอบวงของสามเหลี่ยมหน้าจั่วคือ26 ซม
ตัวอย่างปัญหา 4
สามเหลี่ยมหน้าจั่วมีความสูง 8 ซม. และฐาน 12 ซม. คำนวณเส้นรอบวงของสามเหลี่ยม
วิธีการแก้:
คุณรู้ไหมว่าความสูงของสามเหลี่ยม h = 8 ซม
ด้านข้างของฐาน a = 12 ซม
ถามว่า เส้นรอบวง = ….?
ตอบ:
K = ด้าน a + ด้าน b + ด้าน c
ไม่ทราบทั้งสองด้านของรูปสามเหลี่ยมเราจึงใช้สูตรพีทาโกรัสเพื่อหาความยาวของด้านนั้น

K = 10 + 10 + 12
K = 32 ซม
ดังนั้น เส้นรอบวงของสามเหลี่ยมหน้าจั่วคือ32 ซม
นี่คือคำอธิบายเกี่ยวกับพื้นที่ของสามเหลี่ยมและปริมณฑลของสามเหลี่ยมพร้อมกับตัวอย่างและการอภิปราย อาจมีประโยชน์.
