
สูตรค่าเบี่ยงเบนมาตรฐานหรือที่เรียกว่าส่วนเบี่ยงเบนมาตรฐานเป็นเทคนิคทางสถิติที่ใช้อธิบายความเป็นเนื้อเดียวกันของกลุ่ม
นอกจากนี้ยังสามารถใช้ค่าเบี่ยงเบนมาตรฐานเพื่ออธิบายวิธีการกระจายข้อมูลในตัวอย่างเช่นเดียวกับความสัมพันธ์ระหว่างจุดแต่ละจุดกับค่าเฉลี่ยหรือค่าเฉลี่ยของตัวอย่าง
ก่อนที่เราจะพูดคุยเพิ่มเติมมีบางสิ่งที่เราต้องรู้ก่อนกล่าวคือ:
ค่าเบี่ยงเบนมาตรฐานของชุดข้อมูลอาจเป็นศูนย์หรือมากกว่าหรือน้อยกว่าศูนย์
ค่าที่แตกต่างกันเหล่านี้มีความหมายดังต่อไปนี้:
- ถ้าค่าเบี่ยงเบนมาตรฐานเป็นศูนย์ค่าตัวอย่างทั้งหมดในชุดข้อมูลจะเท่ากัน
- ในขณะเดียวกันค่าเบี่ยงเบนมาตรฐานที่มากกว่าหรือน้อยกว่าศูนย์แสดงว่าจุดข้อมูลของแต่ละบุคคลอยู่ห่างจากค่าเฉลี่ย

ขั้นตอนในการหาค่าเบี่ยงเบนมาตรฐาน
ในการกำหนดและค้นหาค่าเบี่ยงเบนมาตรฐานเราต้องทำตามขั้นตอนด้านล่าง
- ขั้นตอนแรก
คำนวณค่าเฉลี่ยหรือค่าเฉลี่ยในแต่ละจุดข้อมูล
คุณทำได้โดยเพิ่มแต่ละค่าในชุดข้อมูลจากนั้นจำนวนจะหารด้วยจำนวนจุดทั้งหมดจากข้อมูล
- ขั้นตอนต่อไป
คำนวณความแปรปรวนของข้อมูลโดยการคำนวณค่าเบี่ยงเบนหรือความแตกต่างสำหรับแต่ละจุดข้อมูลจากค่าเฉลี่ย
จากนั้นค่าเบี่ยงเบนในแต่ละจุดข้อมูลจะถูกยกกำลังสองและลบออกด้วยกำลังสองของค่าเฉลี่ย
หลังจากได้ค่าความแปรปรวนแล้วเราสามารถคำนวณค่าเบี่ยงเบนมาตรฐานได้โดยการรูทค่าความแปรปรวน
อ่านเพิ่มเติม: คำบรรยาย: ความหมายวัตถุประสงค์ลักษณะประเภทและตัวอย่างสูตรการเบี่ยงเบนมาตรฐาน
1. ค่าเบี่ยงเบนมาตรฐานของประชากร
ประชากรมีสัญลักษณ์โดยσ (ซิกม่า) และสามารถกำหนดได้ด้วยสูตร:

2. ค่าเบี่ยงเบนตัวอย่างมาตรฐาน
สูตรคือ:
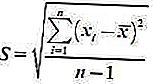
3. สูตรสำหรับส่วนเบี่ยงเบนมาตรฐานของกลุ่มข้อมูลจำนวนมาก
ในการค้นหาการกระจายของข้อมูลจากตัวอย่างเราสามารถลดค่าข้อมูลแต่ละค่าด้วยค่าเฉลี่ยจากนั้นผลลัพธ์ทั้งหมดจะถูกเพิ่ม
อย่างไรก็ตามหากคุณใช้วิธีการข้างต้นผลลัพธ์จะเป็นศูนย์เสมอดังนั้นจึงไม่สามารถใช้วิธีนั้นได้

เพื่อให้ผลลัพธ์ไม่เป็นศูนย์ (0) จากนั้นเราต้องยกกำลังสองการลบของค่าข้อมูลและค่าเฉลี่ยจากนั้นจึงรวมผลลัพธ์ทั้งหมด
เมื่อใช้วิธีนี้ผลลัพธ์ของผลรวมของกำลังสองจะมีค่าเป็นบวก

ค่าของความแปรปรวนจะหาได้จากการหารผลรวมของกำลังสองด้วยจำนวนขนาดข้อมูล (n)
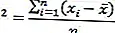
อย่างไรก็ตามหากเราใช้ค่าตัวแปรนี้เพื่อค้นหาความแปรปรวนของประชากรค่าความแปรปรวนจะมากกว่าตัวแปรตัวอย่าง
เพื่อเอาชนะสิ่งนี้ขนาดข้อมูล (n) เป็นตัวแบ่งต้องถูกแทนที่ด้วยองศาอิสระ (n-1) เพื่อให้ค่าความแปรปรวนของตัวอย่างเข้าใกล้ตัวแปรประชากร
ดังนั้นสูตรตัวแปรตัวอย่างสามารถเขียนเป็น:

ค่าของตัวแปรที่ได้รับคือค่ากำลังสองดังนั้นเราต้องยกกำลังสองก่อนเพื่อให้ได้ค่าเบี่ยงเบนมาตรฐาน

เพื่อให้การคำนวณง่ายขึ้นสูตรสำหรับความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานสามารถลดลงเป็นสูตรด้านล่าง
สูตรตัวแปรข้อมูล
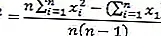
สูตรเบี่ยงเบนมาตรฐาน
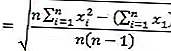
หมายเหตุ :
s2 = ตัวแปร
s = ค่าเบี่ยงเบนมาตรฐาน
x i = ค่าith x
n = ขนาดตัวอย่าง
ตัวอย่างปัญหา Standard Deviation
ต่อไปนี้เป็นตัวอย่างและการแก้ไขปัญหาส่วนเบี่ยงเบนมาตรฐาน
คำถาม:
ซานดีในฐานะประธานของสมาชิกนอกหลักสูตรได้รับหน้าที่บันทึกความสูงโดยรวมของสมาชิก ข้อมูลที่รหัสผ่านเก็บรวบรวมมีดังนี้:
167, 172, 170, 180, 160, 169, 170, 173, 165, 175
จากข้อมูลด้านบนคำนวณค่าเบี่ยงเบนมาตรฐาน!
อ่านเพิ่มเติม: รหัสมอร์ส: ประวัติสูตรและวิธีการท่องจำคำตอบ :
| ผม | x ผม | x ผม 2 |
| 1 | 167 | 27889 |
| 2 | 172 | 29584 |
| 3 | 170 | 28900 |
| 4 | 180 | 32400 |
| 5 | 160 | 25600 |
| 6 | 169 | 28561 |
| 7 | 170 | 28900 |
| 8 | 173 | 29929 |
| 9 | 165 | 27225 |
| 10 | 175 | 30625 |
| Σ | 1710 | 289613 |
จากข้อมูลด้านบนจะเห็นได้ว่าจำนวนข้อมูล (n) = 10 และองศาอิสระ (n-1) = 9 เช่นกัน
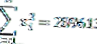
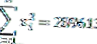
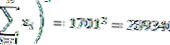
เพื่อให้เราสามารถคำนวณค่าความแปรปรวนได้ดังนี้

ค่าแตกต่างจากข้อมูลที่รวบรวม Sandi เป็น30.32 ในการคำนวณค่าเบี่ยงเบนมาตรฐานเราต้องยกกำลังสองของค่าความแปรปรวนเพื่อให้:
s = √30.32 = 5.51
ดังนั้นค่าเบี่ยงเบนมาตรฐานของปัญหาข้างต้นคือ5.51
ประโยชน์และการใช้งาน
นักสถิตินิยมใช้ค่าเบี่ยงเบนมาตรฐานเพื่อพิจารณาว่าข้อมูลที่นำมาเป็นตัวแทนของประชากรทั้งหมดหรือไม่

ตัวอย่างเช่นมีคนต้องการทราบน้ำหนักของเด็กวัยหัดเดินอายุ 3-4 ปีในหมู่บ้านแห่งหนึ่ง
ดังนั้นเพื่อให้ง่ายขึ้นเราต้องหาน้ำหนักของเด็กสองสามคนแล้วคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน
จากค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานเราสามารถแทนน้ำหนักตัวทั้งหมดของเด็กอายุ 3-4 ปีในหมู่บ้านได้
ข้อมูลอ้างอิง
- Standard Deviation - สูตรสำหรับวิธีค้นหาและตัวอย่างของปัญหา
- Standard Deviation: สูตรการคำนวณและปัญหาตัวอย่าง
