สมการวงกลม - สูตรรูปแบบทั่วไปและปัญหาตัวอย่าง

สมการวงกลมมีรูปแบบทั่วไป x ^ 2 + y ^ 2 + Ax + By + C = 0 ซึ่งสามารถใช้เพื่อกำหนดรัศมีและจุดศูนย์กลางของวงกลม

สมการวงกลมที่คุณจะได้เรียนรู้ด้านล่างนี้มีหลายรูปแบบ ในกรณีที่แตกต่างกันสมการอาจแตกต่างกัน ดังนั้นควรทำความเข้าใจให้ดีเพื่อที่คุณจะได้จดจำมันด้วยใจ

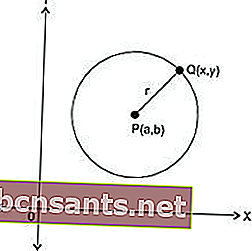
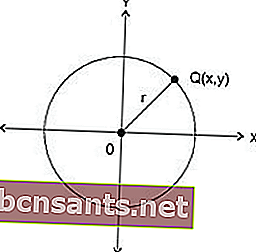
วงกลมคือชุดของจุดที่ห่างจากจุดหนึ่งเท่ากัน พิกัดของจุดเหล่านี้ถูกกำหนดโดยการจัดเรียงของสมการ โดยพิจารณาจากความยาวของรัศมีและพิกัดของศูนย์กลางของวงกลม

สมการวงกลม

มีหลายชนิดของสมการคือสมการที่เกิดจากจุดศูนย์กลางและรัศมีและสมการที่สามารถพบได้สำหรับจุดศูนย์กลางและรัศมี

สมการวงกลมทั่วไป

มีสมการทั่วไปดังต่อไปนี้:

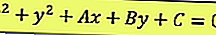
เมื่อพิจารณาจากสมการข้างต้นสามารถกำหนดจุดศูนย์กลางและรัศมีได้ดังนี้

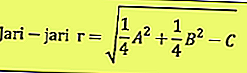
ศูนย์กลางของวงกลมคือ:

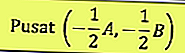
ที่ศูนย์กลางของ P (a, b) และรัศมี r

จากวงกลมถ้าคุณรู้จุดศูนย์กลางและรัศมีคุณจะได้สูตร:

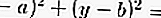
ถ้าคุณรู้จุดศูนย์กลางของวงกลมและรัศมีของวงกลมโดยที่ (a, b) เป็นศูนย์กลางและ r คือรัศมีของวงกลม

จากสมการที่ได้รับข้างต้นเราสามารถระบุได้ว่ารวมจุดที่อยู่บนวงกลมหรือภายในหรือภายนอก ในการกำหนดตำแหน่งของจุดโดยใช้การแทนที่จุดในตัวแปร x และ y จากนั้นเปรียบเทียบผลลัพธ์กับกำลังสองของรัศมีของวงกลม

จุด M (x ₁ , y ₁ ) อยู่:

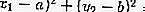
บนวงกลม:

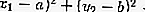
ภายในวงกลม:

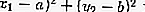
นอกวงกลม:

ที่โดยมีศูนย์กลาง O (0,0) และรัศมี r

หากจุดศูนย์กลางอยู่ที่ O (0,0) ให้ทำการแทนที่ในส่วนก่อนหน้า ได้แก่ :

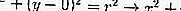
จากสมการข้างต้นสามารถกำหนดตำแหน่งของจุดบนวงกลมได้

จุด M (x ₁ , y ₁ ) อยู่:

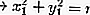
บนวงกลม:

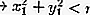
ภายในวงกลม:

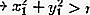
นอกวงกลม: อ่านเพิ่มเติม: Art Is: คำจำกัดความฟังก์ชันประเภทและตัวอย่าง [FULL]

รูปแบบทั่วไปของสมการสามารถแสดงได้ในรูปแบบต่อไปนี้

(x - a) 2 + (y - b) 2 = r2 หรือ

X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0 หรือ

X2 + y2 + px + Qy + S = 0 โดยที่ P = -2a, Q = -2b และ S = a2 + b2 - r2

จุดตัดของเส้นและวงกลม

วงกลมที่มีสมการ x2 + y2 + Ax + By + C = 0 สามารถกำหนดได้ว่าเส้น h ที่มีสมการ y = mx + n ไม่แตะต้องทำให้ขุ่นเคืองหรือตัดกันโดยใช้หลักการเลือกปฏิบัติ

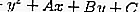
……. (สมการ 1)

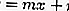
…… .. (สมการ 2)

โดยการแทนสมการ 2 เป็นสมการ 1 คุณจะได้สมการกำลังสองคือ:

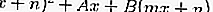
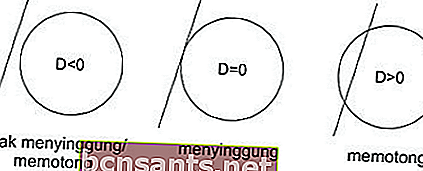
จากสมการกำลังสองข้างต้นโดยการเปรียบเทียบค่าการจำแนกจะเห็นได้ว่าเส้นนั้นไม่ทำให้ขุ่นเคืองทำให้ขุ่นเคืองหรือตัดกัน

เส้น h ไม่ตัดกัน / ทำให้วงกลมขุ่นเคืองดังนั้น D <0

เส้น h แทนเจนต์กับวงกลมดังนั้น D = 0

เส้น h ตัดกับวงกลมดังนั้น D> 0

สมการของแทนเจนต์เป็นวงกลม

1. สมการของเส้นสัมผัสผ่านจุดบนวงกลม

สัมผัสกับวงกลมตรงกับจุดที่อยู่บนวงกลม จากจุดตัดกันของเส้นสัมผัสและวงกลมสามารถกำหนดสมการของเส้นสัมผัสได้

สมการแทนเจนต์กับวงกลมผ่านจุด P (x ₁ , y ₁ ) สามารถกำหนดได้กล่าวคือ:

• รูปร่าง

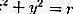
สมการของแทนเจนต์

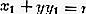
• รูปร่าง

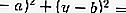
สมการของแทนเจนต์

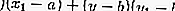
• รูปร่าง

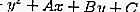
สมการของแทนเจนต์

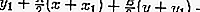
ตัวอย่างปัญหา:

สมการแทนเจนต์ผ่านจุด (-1,1) บนวงกลม

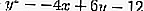
คือ:

ตอบ:

รู้สมการของวงกลม

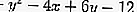
โดยที่ A = -4, B = 6 และ C = -12 และ x ₁ = -1, y ₁ = 1

PGS คือ

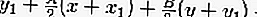
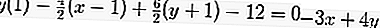
สมการของแทนเจนต์คือ

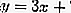
2. สมการแทนเจนต์กับการไล่ระดับสี

ถ้าเส้นที่มีความชัน m สัมผัสกับวงกลม

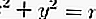
จากนั้นสมการของแทนเจนต์คือ:

ถ้าเป็นวงกลม

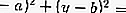
จากนั้นสมการของแทนเจนต์:

ถ้าเป็นวงกลม

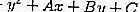
จากนั้นสมการของแทนเจนต์โดยการแทนที่ r ด้วย

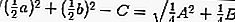
ดังนั้น:

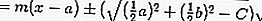
หรือ

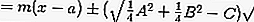
3. สมการของเส้นสัมผัสกับจุดนอกวงกลม

จากจุดที่อยู่นอกวงกลมสามารถวาดเส้นสัมผัสสองเส้นถึงวงกลมได้

อ่านเพิ่มเติม: ประชาธิปไตย: ความหมายประวัติศาสตร์และประเภท [เต็ม]

ในการหาสมการแทนเจนต์จะใช้สูตรสมการเส้นตรง ได้แก่ :

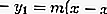
อย่างไรก็ตามจากสูตรนี้ไม่ทราบค่าของความชันของเส้น ในการหาความชันของเส้นตรงให้แทนที่สมการของสมการวงกลม เนื่องจากเส้นเป็นแทนเจนต์ดังนั้นจากสมการจะได้ผลลัพธ์การแทนค่า D = 0 และค่าของ m จะได้รับ

ตัวอย่างปัญหา

ตัวอย่างปัญหา 1

วงกลมมีจุดศูนย์กลาง (2, 3) และมีเส้นผ่านศูนย์กลาง 8 ซม. สมการของวงกลมคือ ...

อภิปรายผล:

เนื่องจาก d = 8 หมายถึง r = 8/2 = 4 ดังนั้นสมการของวงกลมที่เกิดขึ้นคือ

(x - 2) ² + (y - 3) ² = 42

x² - 4x + 4 + y² -6y + 9 = 16

x² + y² - 4x - 6y - 3 = 0

ตัวอย่างปัญหา 2

กำหนดสมการทั่วไปสำหรับวงกลมที่มีศูนย์กลางอยู่ที่จุด (5,1) และขีดเส้นตรง 3 x - 4 y + 4 = 0!

อภิปรายผล:

ถ้าทราบว่าจุดศูนย์กลางของวงกลม ( a , b ) = (5,1) และแทนเจนต์ของวงกลมคือ 3 x - 4 y + 4 = 0 รัศมีของวงกลมจะถูกกำหนดดังนี้

ดังนั้นสมการทั่วไปของวงกลมจึงเป็นดังนี้

ดังนั้นสมการทั่วไปของวงกลมที่มีศูนย์กลางอยู่ที่ (5,1) และทำให้เส้นตรง 3 x - 4 y + 4 = 0 คือ

ตัวอย่างปัญหา 3

ค้นหาสมการทั่วไปของวงกลมที่มีศูนย์กลางอยู่ที่ (-3,4) และทำให้แกน Y ขุ่นเคือง!

อภิปรายผล:

ก่อนอื่นเรามาวาดกราฟของวงกลมก่อนซึ่งมีศูนย์กลางอยู่ที่ (-3,4) และทำให้แกน Y ขุ่นเคือง!

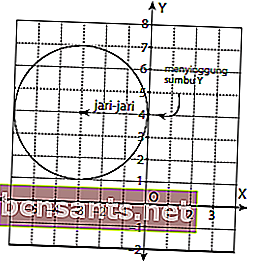
จากภาพด้านบนจะเห็นได้ว่าจุดศูนย์กลางของวงกลมอยู่ที่พิกัด (-3,4) โดยมีรัศมี 3 ดังนั้น:

ดังนั้นสมการทั่วไปที่อยู่กึ่งกลาง (-3,4) และทำให้แกน Y ผิดปกติคือ

ในบางกรณีไม่ทราบรัศมีของวงกลม แต่ทราบแทนเจนต์ แล้วจะกำหนดรัศมีของวงกลมได้อย่างไร? ดูภาพต่อไปนี้

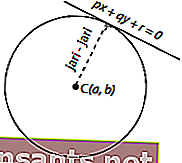
ภาพด้านบนแสดงให้เห็นว่าแทนเจนต์ของสมการpx + qy + r = 0 เกี่ยวข้องกับวงกลมที่อยู่ตรงกลาง C ( a, b ) รัศมีสามารถกำหนดได้โดยสมการต่อไปนี้ ก, ข ). รัศมีสามารถกำหนดได้โดยสมการต่อไปนี้

อาจมีประโยชน์.