
สมการกำลังสองเป็นหนึ่งในสมการทางคณิตศาสตร์ของตัวแปรที่มีกำลังสองสูงสุด
รูปแบบทั่วไปของสมการกำลังสองหรือ PK มีดังนี้:
ขวาน2 + bx + c = 0
โดยที่xเป็นตัวแปรa , b คือสัมประสิทธิ์และc คือค่าคงที่ ค่าของ a ไม่เท่ากับศูนย์
รูปร่างกราฟ
หากอธิบายสมการกำลังสองในรูปของพิกัดคาร์ทีเซียน (x, y) มันจะสร้างกราฟพาราโบลา ดังนั้นสมการกำลังสองก็มักจะเรียกว่าสมการพาราโบลา
ต่อไปนี้เป็นตัวอย่างของรูปแบบของสมการนี้ในรูปของกราฟพาราโบลา
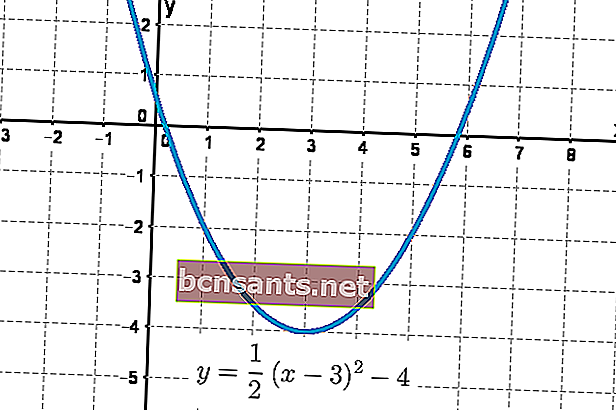
ในสมการทั่วไปค่าของa , bและcมีผลต่อรูปแบบพาราโบลาที่เป็นผลลัพธ์อย่างมาก
ค่าของaกำหนดส่วนโค้งเว้าหรือนูนของพาราโบลา ถ้าค่าของA> 0แล้วพาราโบลาจะเปิดขึ้น (เว้า) ตรงกันข้ามถ้าค่า <0แล้วพาราโบลาจะเปิดลง (นูน)

ค่าของขสมการกำหนดจุดสุดยอดของรูปโค้งที่ ในคำอื่น ๆ กำหนดมูลค่าของแกนสมมาตรของเส้นโค้งซึ่งเท่ากับx = - B / 2a

ค่าคงที่คบนกราฟของสมการกำหนดจุดตัดของฟังก์ชั่นโค้งบนแกน y ต่อไปนี้เป็นกราฟพาราโบลาที่มีการเปลี่ยนแปลงในมูลค่าคงค

รากของสมการกำลังสอง (PK)
วิธีการแก้สมการที่ถูกเรียกว่าkar ที่รากของสมการ
PK Roots ต่างๆ
ชนิดของราก PK สามารถพบได้ง่ายโดยใช้สูตรทั่วไป D = b2 - 4ac จากสมการทั่วไปสำหรับกำลังสอง ax2 + bx + c = 0
ต่อไปนี้เป็นชนิดของรากของสมการกำลังสอง
1. รูทจริง (D> 0)
ถ้าค่า D> 0 จาก PK มันจะสร้างรากจริง แต่มีรากต่างกัน กล่าวอีกนัยหนึ่ง x1 ไม่เหมือนกับ x2
ตัวอย่างสมการรากจริง (D> 0)
หาประเภทรากของสมการ x2 + 4x + 2 = 0
การตั้งถิ่นฐาน:
ก = 1; b = 4; และ c = 2
D = b2 - 4ac
D = 42 - 4 (1) (2)
D = 16 - 8
D = 8
ดังนั้นเนื่องจากค่าของ D> 0 ดังนั้นรูทจึงเป็นประเภทรูทจริง
2. รูทจริงเท่ากับ x1 = x2 (D = 0)
เป็นรากชนิดหนึ่งของสมการกำลังสองที่สร้างรากที่มีค่าเท่ากัน (x1 = x2)
ตัวอย่างรากจริง (D = 0)
ค้นหาค่ารูท PK ของ 2x2 + 4x + 2 = 0
อ่านเพิ่มเติม: ประเภทของวัฏจักรของน้ำ (+ รูปภาพเต็มและคำอธิบาย)การตั้งถิ่นฐาน:
ก = 2; b = 4; c = 2
D = b2 - 4ac
D = 42 - 4 (2) (2)
D = 16 - 16
D = 0
ดังนั้นเนื่องจากค่าของ D = 0 จึงได้รับการพิสูจน์แล้วว่ารากเป็นของจริงและเป็นคู่กัน
3. รากในจินตนาการ / ไม่จริง (D <0)
ถ้าค่าของ D <0 รากของสมการกำลังสองจะเป็นจินตภาพ / ไม่ใช่จริง
ตัวอย่างรากจินตภาพ (D <0) /
หาประเภทรากของสมการ x2 + 2x + 4 = 0
การตั้งถิ่นฐาน:
ก = 1; b = 2; c = 4
D = b2 - 4ac
D = 22 - 4 (1) (4)
D = 4 - 16
D = -12
ดังนั้นเนื่องจากค่าของ D <0 รากของสมการจึงเป็นรากที่ไม่จริงหรือในจินตนาการ
ค้นหารากของสมการกำลังสอง
มีหลายวิธีที่สามารถใช้เพื่อค้นหารากของสมการกำลังสอง ในหมู่พวกเขามีการแยกตัวประกอบกำลังสองสมบูรณ์และใช้สูตร abc
ต่อไปนี้อธิบายถึงวิธีการต่างๆในการค้นหารากสมการ
1. การแยกตัวประกอบ
การแยกตัวประกอบ / การแยกตัวประกอบเป็นวิธีการหารากโดยการหาค่าซึ่งถ้าคูณกันจะทำให้เกิดค่าอื่น
สมการกำลังสอง (PK) มีสามรูปแบบที่มีการแยกตัวประกอบของรากที่แตกต่างกัน ได้แก่ :
| ไม่ | แบบสมการ | Root-Root Factorization |
| 1 | x 2 + 2xy + y 2 = 0 | (x + y) 2 = 0 |
| 2 | x 2 - 2xy + y 2 = 0 | (x - y) 2 = 0 |
| 3 | x 2 - y 2 = 0 | (x + y) (x - y) = 0 |
ต่อไปนี้เป็นตัวอย่างปัญหาเกี่ยวกับการใช้วิธีการแยกตัวประกอบในสมการกำลังสอง
แก้สมการกำลังสอง 5x 2 + 13x + 6 = 0 โดยใช้วิธีแยกตัวประกอบ
การตั้งถิ่นฐาน:
5x2 + 13x = 6 = 0
5x2 + 10x + 3x + 6 = 0
5x (x + 2) + 3 (x + 2) = 0
(5x + 3) (x + 2) = 0
5x = -3 หรือ x = -2
ดังนั้นผลลัพธ์ของการแก้ปัญหาคือ x = -3/5 หรือ x = -2
2. กำลังสองที่สมบูรณ์แบบ
กำลังสองสมบูรณ์แบบรูปแบบเป็นสมการที่ก่อให้สรุปตัวเลข
ผลลัพธ์ของสมการกำลังสองสมบูรณ์โดยทั่วไปใช้สูตรต่อไปนี้:
(x + p) 2 = x2 + 2px + p2
คำตอบทั่วไปสำหรับสมการกำลังสองสมบูรณ์มีดังนี้:
(x + p) 2 = x2 + 2px + p2
ด้วย (x + p) 2 = q แล้ว:
(x + p) 2 = q
x + p = ± q
x = -p ± q
ต่อไปนี้เป็นตัวอย่างปัญหาเกี่ยวกับการใช้วิธีสมการสมบูรณ์แบบ
แก้สมการ x2 + 6x + 5 = 0 โดยใช้วิธีสมการกำลังสองสมบูรณ์แบบ!
การตั้งถิ่นฐาน:
x2 + 6x +5 = 0
x2 + 6x = -5
ขั้นตอนต่อไปคือการเพิ่มตัวเลขหนึ่งตัวทางด้านขวาและด้านซ้ายเพื่อให้สามารถเปลี่ยนเป็นกำลังสองที่สมบูรณ์แบบได้
x2 + 6x + 9 = -5 + 9
x2 + 6x + 9 = 4
(x + 3) 2 = 4
(x + 3) = √4
x = 3 ± 2
ดังนั้นผลลัพธ์สุดท้ายคือ x = -1 หรือ x = -5
อ่านเพิ่มเติม: ความหมายและความแตกต่างของคำพ้องเสียงคำพ้องเสียงและคำพ้องเสียง3. สูตร ABC กำลังสอง
สูตร abc เป็นทางเลือกอื่นเมื่อไม่สามารถแก้สมการกำลังสองโดยการแยกตัวประกอบหรือวิธีกำลังสองที่สมบูรณ์แบบ
ต่อไปนี้เป็นสูตรabcสำหรับสมการกำลังสอง ax2 + bx + c = 0
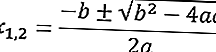
นี่คือตัวอย่างของการแก้ปัญหาโดยใช้สมการที่abcสูตร
แก้สมการ x2 + 4x - 12 = 0 โดยใช้วิธีสูตร abc!
การตั้งถิ่นฐาน:
x2 + 4x - 12 = 0
โดยที่ a = 1, b = 4, c = -12

การสร้างสมการกำลังสองใหม่
หากเราเคยเรียนรู้วิธีการหารากของสมการมาก่อนตอนนี้เราจะเรียนรู้ที่จะสร้างสมการกำลังสองจากรากที่เคยรู้มาก่อน
นี่คือสองสามวิธีในการสร้าง PK ใหม่
1. สร้างสมการเมื่อทราบราก
ถ้าสมการมีราก x1 และ x2 สมการของรากเหล่านั้นสามารถแสดงในรูปของ
(x- x 1 ) (x- x 2 ) = 0
ตัวอย่าง:
หาสมการกำลังสองที่รากอยู่ระหว่าง -2 ถึง 3
การตั้งถิ่นฐาน:
x 1 = -2 และ x 2 = 3
(x - (- 2)) (x-3) = 0
(x + 2) (x + 3)
x2-3x + 2x-6 = 0
x2-x-6 = 0
ดังนั้นผลลัพธ์ของสมการสำหรับรากเหล่านี้คือ x2-x-6 = 0
2. สร้างสมการกำลังสองถ้าคุณรู้จำนวนและผลคูณของราก
ถ้าทราบรากของสมการกำลังสองที่มีจำนวนและคูณ x1 และ x2 สมการกำลังสองสามารถแปลงเป็นรูปแบบต่อไปนี้ได้
x2- (x 1+ x 2 ) x + (x 1. x 2 ) = 0
ตัวอย่าง:
หาสมการกำลังสองที่มีราก 3 และ 1/2
การตั้งถิ่นฐาน:
x 1 = 3 และ x 2 = -1/2
x 1+ x 2 = 3 -1/2 = 6/2 - 1/2 = 5/2
x 1. x 2 = 3 (-1/2) = -3/2
ดังนั้นสมการกำลังสองคือ:
x2- (x 1+ x 2 ) x + (x 1. x 2 ) = 0
x2– 5/2 x - 3/2 = 0 (แต่ละด้านคูณด้วย 2)
2x2-5x-3 = 0
ดังนั้นสมการกำลังสองสำหรับราก 3 และ 1/2 คือ 2x2-5x-3 = 0
