
ความหนาแน่นหรือความหนาแน่นของมวลเป็นการวัดความหนาแน่นของมวลต่อหน่วยปริมาตรของวัตถุ ยิ่งวัตถุมีมวลมากเท่าใดมวลของแต่ละปริมาตรก็จะยิ่งมากขึ้นเท่านั้น
คุณเคยเห็นเรือที่ลอยอยู่บนน้ำหรือไม่? เรือที่ทำจากไม้สามารถลอยน้ำได้เนื่องจากความหนาแน่นของไม้มีขนาดเล็กกว่าความหนาแน่นของน้ำ

จากนั้นน้ำมันที่ผสมกับน้ำในแก้วจะแยกสารออกมาและลอยอยู่บนน้ำ ทั้งนี้เนื่องจากความหนาแน่นของน้ำมากกว่าน้ำมัน
แนวคิดเรื่องความหนาแน่นสามารถกำหนดได้ว่าวัตถุหนักหรือเบาเพียงใดเมื่อเทียบกับปริมาตร ต่อไปนี้เป็นการอภิปรายเพิ่มเติมเกี่ยวกับความหนาแน่นมวลของวัตถุ
สูตรและหน่วย
ในการกำหนดความหนาแน่นของวัตถุคุณสามารถใช้สูตรหรือสมการด้านล่าง:

ความหนาแน่นที่เป็นสัญลักษณ์โดยρจะอ่านว่า "rho" ในภาพด้านบน สูตรสำหรับความหนาแน่นเป็นผลมาจากการหารมวลของวัตถุด้วยปริมาตรของวัตถุ
หน่วยความหนาแน่นตามระบบสากลของหน่วยคือ Kg / m3 หรือ Kg m - 3 มวลเป็นกิโลกรัมและปริมาตรเป็น m3
การแปลงหน่วยอื่น ๆ มีดังนี้
- 1 Kg / m3 = 0.001 g / cm3
- 1 ก. / ซม. 3 = 1,000 กก. / ลบ.ม.
- 1 ลิตร = 1,000 มิลลิลิตร = 1,000 ซม. 3
แล้วอะไรคือความแตกต่างระหว่างมวลและความหนาแน่นของวัตถุ?
คำตอบ:
มวลแสดงจำนวนอนุภาคที่สามารถพบได้บนวัตถุในขณะที่ความหนาแน่นจะบอกให้คุณทราบว่าอนุภาคนั้นมีความหนาแน่นมากเพียงใด

การวัดความหนาแน่น
การวัดความหนาแน่นของวัตถุเราต้องวัดมวลของวัตถุและวัดปริมาตรของวัตถุ
- มวลของวัตถุถูกวัดโดยสมดุล
- วัดปริมาตรได้หลายวิธี
ถ้าวัตถุนั้นมีรูปร่างปกติเช่นลูกบาศก์บล็อกหรือทรงกลมเราสามารถวัดความยาวด้านข้างแล้วคำนวณปริมาตรโดยใช้สูตรสำหรับปริมาตรของลูกบาศก์บล็อกหรือทรงกลม
แต่ถ้าวัตถุที่คุณกำลังวัดมีรูปร่างผิดปกติเช่นหินให้ใช้ถ้วยตวงเพื่อวัดปริมาตร
- ความหนาแน่นหาได้จากการหารมวลของวัตถุด้วยปริมาตร
สิ่งที่คุณต้องรู้คือวัตถุทุกชิ้นมีความหนาแน่นของมวลที่แตกต่างกัน ความหนาแน่นของมวลจะเป็นตัวกำหนดว่าวัสดุมีความหนาแน่นหรือแข็งเพียงใด นี่คือความหนาแน่นมวลของวัสดุและวัสดุต่างๆ
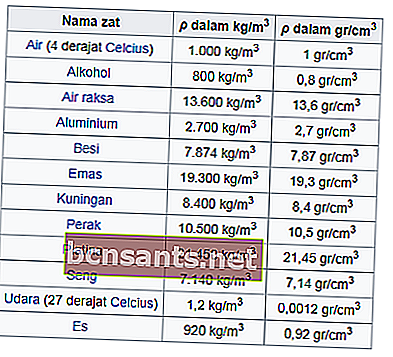
ตัวอย่างปัญหา
1. วัสดุชนิด X เป็นลูกบาศก์ด้านละ 4 ม. ชั่งวัสดุด้วยเครื่องชั่งน้ำหนัก 2 Kg. ความหนาแน่นหรือความหนาแน่นมวลของวัตถุ X คืออะไร?
การตั้งถิ่นฐาน
ระบุว่ามวล = 2 Kg และปริมาตรของทรงลูกบาศก์ = 43 = 16
เพื่อให้ความหนาแน่นมวลของวัสดุคือρ = 2/16 = 0.125 Kg / m3
2. น้ำมีมวลเท่าไหร่ถ้ามีปริมาตร 1 ลิตร?
การตั้งถิ่นฐาน
เป็นที่รู้จัก
V = 1 ลิตร = 0.001 m³
จากตารางρน้ำ = 1,000 Kg / m3
ดังนั้นโดยใช้สมการความหนาแน่นจะได้รับ:
ม = ρ V = (1000) (0.001) = 1 กก
3. เหล็กที่มีรูปร่างผิดปกติจะชั่งให้มีน้ำหนัก 14 Kg. ปริมาตรของเตารีดจะวัดด้วยถ้วยตวงที่เต็มไปด้วยน้ำ ก่อนเติมเหล็กปริมาณน้ำจะตรงตามถ้วยตวง หลังจากใส่เหล็กแล้วน้ำในแก้วจะหก ปริมาณน้ำที่หก?
วิธีแก้ไข :
มวลหิน (ม.) = 14 Kg
ความหนาแน่นρเหล็ก = 7,874 Kg / m³
ปริมาตรของหินที่ใส่ลงในถ้วยตวงที่เต็มไปด้วยน้ำทำให้น้ำในแก้วสูญเปล่า นั่นหมายความว่าปริมาตรน้ำที่หก = ปริมาตรของหิน
v = ม. / ρ = 14 / 7,874 = 1.77 ม.
ดังนั้นน้ำที่เสียไปคือ 1.77 ม.
