
ค่าสัมบูรณ์ในแคลคูลัสมีประโยชน์มากสำหรับการแก้ปัญหาทางคณิตศาสตร์ต่างๆทั้งในสมการและอสมการ ต่อไปนี้เป็นคำอธิบายที่สมบูรณ์เกี่ยวกับค่าสัมบูรณ์และคำถามตัวอย่าง
คำจำกัดความของค่าสัมบูรณ์
ตัวเลขทั้งหมดมีค่าสัมบูรณ์ตามลำดับ จำนวนสัมบูรณ์ทั้งหมดเป็นค่าบวกดังนั้นค่าจำนวนสัมบูรณ์ของตัวเลขที่มีจำนวนเดียวกัน แต่ความแตกต่างระหว่างสัญกรณ์บวก (+) และลบ (-) จะมีผลลัพธ์จำนวนสัมบูรณ์เหมือนกัน
ถ้า x เป็นสมาชิกของจำนวนจริงค่าสัมบูรณ์จะเขียนเป็น | x | และกำหนดไว้ดังนี้:

"ค่าสัมบูรณ์คือตัวเลขที่มีค่าความยาวหรือระยะทางเท่ากันจากจุดกำเนิดหรือจุดศูนย์ในพิกัด"
สามารถตีความได้ว่าค่าสัมบูรณ์ของ 5 คือความยาวหรือระยะทางจากจุด 0 ถึงจุด 5 หรือ (-5)
ค่าสัมบูรณ์ของ (-9) และ 9 คือ 9 ค่าสัมบูรณ์ของ 0 คือ 0 และอื่น ๆ Nilaa
ฉันจะเข้าใจมันอย่างแน่นอนโดยดูภาพต่อไปนี้:

ในภาพด้านบนสามารถเข้าใจได้ว่าค่าของ | 5 | คือระยะห่างของจุด 5 จากเลข 0 คือ 5 และ | -5 | ระยะห่างของจุด (-5) จากหมายเลข 0 คือ 5
ถ้า | x | แสดงระยะทางจากจุด x ถึง 0 แล้ว | xa | คือระยะทางจากจุด x ถึงจุด a ตัวอย่างเช่นเมื่อแสดงระยะทางจากจุดที่ 5 ถึงจุดที่ 2 อาจเขียนเป็น | 5-2 | = 3

โดยทั่วไปสามารถระบุได้ว่าระยะทาง x ถึง a สามารถเขียนได้ด้วยสัญกรณ์ | xa | หรือ | ขวาน |
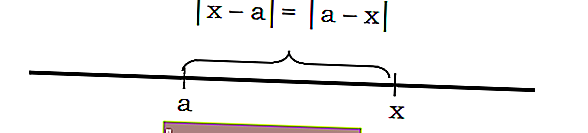
ตัวอย่างเช่นระยะห่างของตัวเลขถึงจุด 3 มีค่า 7 ดังนี้:
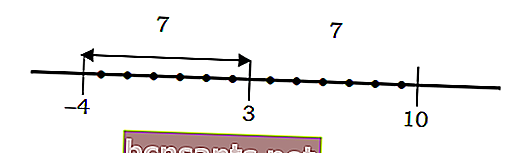
หากอธิบายไว้ในสมการพีชคณิต | x-3 | = 7 จะสามารถแก้ไขได้ดังนี้:
อ่านเพิ่มเติม: การวัดแผ่นดินไหวด้วยลอการิทึม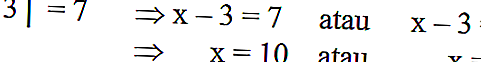
จำไว้ว่า | x-3 | คือระยะห่างของจำนวน x ถึงจุด 3 โดยที่ | x-3 | = 7 คือระยะห่างของจำนวน x ถึงจุด 3 ตาม 7 หน่วย
คุณสมบัติของค่าสัมบูรณ์
ในการดำเนินการสมการจำนวนสัมบูรณ์มีคุณสมบัติจำนวนสัมบูรณ์ที่สามารถช่วยแก้สมการจำนวนสัมบูรณ์ได้
คุณสมบัติของจำนวนสัมบูรณ์โดยทั่วไปในสมการค่าสัมบูรณ์มีดังนี้

คุณสมบัติของค่าสัมบูรณ์ของอสมการ:
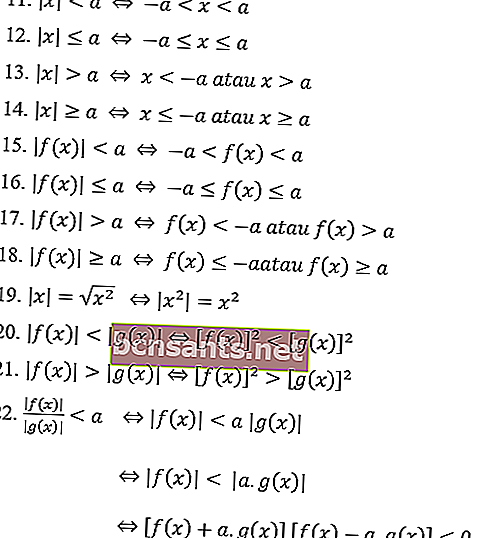
ตัวอย่างปัญหาสมการค่าสัมบูรณ์
ตัวอย่างปัญหา 1
ค่าสัมบูรณ์ของสมการคืออะไร | 10-3 |?
ตอบ:
| 10-3 | = | 7 | = 7
ตัวอย่างปัญหา 2
ผลลัพธ์ของ x สำหรับสมการสำหรับค่าสัมบูรณ์ | x-6 | = 10 คืออะไร?
ตอบ:
เพื่อแก้สมการนี้มีสองผลลัพธ์ที่เป็นไปได้สำหรับจำนวนสัมบูรณ์
| x-6 | = 10
วิธีแก้ปัญหาแรก:
x-6 = 10
x = 16
วิธีที่สอง:
x - 6 = -10
x = -4
ดังนั้นคำตอบของสมการนี้คือ 16 หรือ (-4)
ตัวอย่างปัญหา 3
แก้และคำนวณค่า x ในสมการต่อไปนี้
–3 | x - 7 | + 2 = –13
ตอบ:
–3 | x - 7 | + 2 = –13
–3 | x - 7 | = –13 - 2
–3 | x - 7 | = –15
| x - 7 | = –15 / –3
| x - 7 | = 5
ทำจนได้โซลูชันด้านบนแล้วค่า x มีสองค่า
x - 7 = 5
x = 12
หรือ
x - 7 = - 5
x = 2
ดังนั้นค่า x สุดท้ายคือ 12 หรือ 2
ตัวอย่างปัญหา 4
แก้สมการต่อไปนี้และค่า x คืออะไร
| 7 - 2x | - 11 = 14
ตอบ:
| 7 - 2x | - 11 = 14
| 7 - 2x | = 14 + 11
| 7 - 2x | = 25
หลังจากทำสมการข้างต้นเสร็จแล้วตัวเลขสำหรับค่าสัมบูรณ์ของ x จะเป็นดังนี้
7 - 2x = 25
2x = - 18
x = - 9
หรือ
7 - 2x = - 25
2x = 32
x = 16
ดังนั้นค่า x สุดท้ายคือ (- 9) หรือ 16
ตัวอย่างปัญหา 5
ค้นหาคำตอบสำหรับสมการค่าสัมบูรณ์ต่อไปนี้:
| 4x - 2 | = | x + 7 |
ตอบ:
ในการแก้สมการข้างต้นให้ใช้คำตอบที่เป็นไปได้สองวิธี ได้แก่ :
อ่านเพิ่มเติม: ข้อผิดพลาดในการอ่านผลทางสถิติของการสำรวจความสามารถในการเลือกตั้งของผู้สมัครชิงตำแหน่งประธานาธิบดี4x - 2 = x + 7
x = 3
หรือ
4x - 2 = - (x + 7)
x = - 1
ดังนั้นคำตอบสำหรับสมการ | 4x - 2 | = | x + 7 | คือ x = 3 หรือ x = - 1
ตัวอย่างปัญหา 6
กำหนดคำตอบสำหรับสมการค่าสัมบูรณ์ต่อไปนี้:
| 3x + 2 | ² + | 3x + 2 | - 2 = 0
ค่า x คืออะไร?
ตอบ:
การทำให้เข้าใจง่าย: | 3x + 2 | = หน้า
แล้ว
| 3x + 2 | ² + | 3x + 2 | -2 = 0
p² + p - 2 = 0
(p + 2) (p - 1) = 0
p + 2 = 0
p = - 2 (ค่าสัมบูรณ์ไม่เป็นลบ)
หรือ
พี - 1 = 0
p = 1
| 3x + 2 | = 1
จนกว่าคำตอบด้านบนจะมีคำตอบที่เป็นไปได้ 2 ข้อสำหรับ x คือ:
3x + 2 = 1
3x = 1 - 2
3x = - 1
x = - 1/3
หรือ
- (3x + 2) = 1
3x + 2 = - 1
3x = - 1 - 2
3x = - 3
x = - 1
ดังนั้นคำตอบของสมการคือ x = - 1/3 หรือ x = - 1
อ้างอิง:ค่าสัมบูรณ์ - คณิตศาสตร์เป็นเรื่องสนุก
