
ไม่มีกำหนดหนึ่งหรือที่เรียกกันว่าป้องกันอนุพันธ์เป็นรูปแบบของการดำเนินงานบูรณาการซึ่งเป็นผู้ผลิตฟังก์ชั่นใหม่
อินทิกรัลมีบทบาทสำคัญมากในคณิตศาสตร์ ทฤษฎีสามารถกำหนดพื้นที่ใต้เส้นโค้งของฟังก์ชันได้
อินทิกรัลมีประโยชน์สำหรับขีด จำกัด ผลรวมที่ต่อเนื่องกับฟังก์ชันต่อเนื่อง อินทิกรัลคือการต่อต้านอนุพันธ์ จากนั้นถ้าfเป็นฟังก์ชันต่อเนื่องผลลัพธ์ที่รวมของฟังก์ชันf จะแสดงเป็น F
ประเภทของอินเทอร์กรัลตามขอบเขตการทำงานบางอย่างไม่แน่นอน ต่อไปนี้เป็นการอภิปรายเกี่ยวกับประเภทของปริพันธ์ที่มีขีด จำกัด ไม่ จำกัด
อินทิกรัลไม่ จำกัด
อินทิกรัลไม่ จำกัด หรือเรียกอีกอย่างว่าแอนตี้ - อนุพันธ์หรือแอนตี้ไดเรนเชียลคือรูปแบบของการดำเนินการรวมที่ก่อให้เกิดฟังก์ชันใหม่
พิจารณาสมการต่อไปนี้

กับ C ค่าคงที่ สูตรอินทิกรัลไม่แน่นอนมีดังนี้
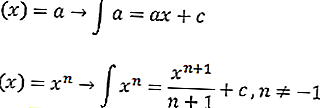
หรือเท่ากับ

ด้วย
- a (x) ^ n = ฟังก์ชันสมการ
- a = ค่าคงที่
- x = ตัวแปร
- n = กำลังของฟังก์ชันสมการ
- C = ค่าคงที่
ผลลัพธ์ของอินทิกรัลไม่ จำกัด นี้คือฟังก์ชันซึ่งเป็นฟังก์ชันใหม่ที่ไม่มีค่าที่แน่นอนหรือแน่นอนเนื่องจากยังมีตัวแปรอยู่ในฟังก์ชันใหม่
เพื่อให้คุณเข้าใจแนวคิดของอินทิกรัลที่ไม่แน่นอนได้ดีขึ้นให้พิจารณาปัญหาตัวอย่างด้านล่าง

จากตัวอย่างนี้สามารถกำหนดรูปแบบการดำเนินการที่สำคัญได้กล่าวคือ
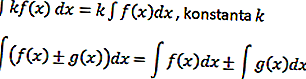
ตรีโกณมิติอินทิกรัล
อินทิกรัลของฟังก์ชันไม่จำเป็นต้องเป็นค่าคงที่เชิงเส้นหรือพหุนาม การแก้ปัญหาระหว่างกันนี้มักเกี่ยวข้องกับองค์ประกอบตรีโกณมิติ
ในฟังก์ชันตรีโกณมิติจะใช้คำจำกัดความของปริพันธ์ที่จัดเรียงในตารางต่อไปนี้ด้วย
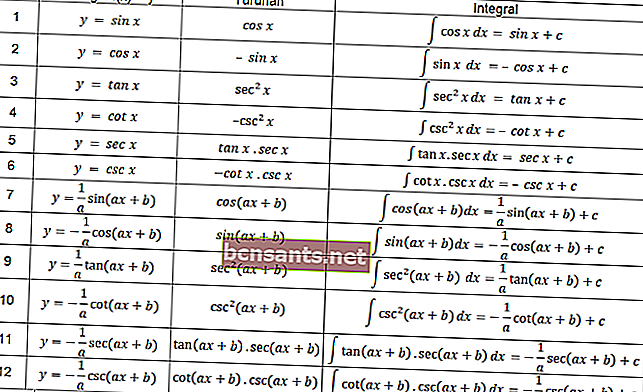
คุณสามารถใช้สมการในตารางด้านบนเพื่อแก้ปัญหาอินทิกรัลที่เกี่ยวข้องกับตรีโกณมิติ
เพื่อให้เข้าใจปริพันธ์ตรีโกณมิติได้ดีขึ้นคุณสามารถเข้าใจตัวอย่างต่อไปนี้
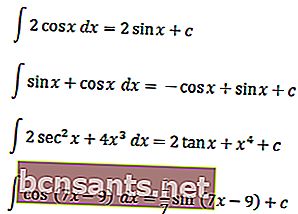
นั่นคือคำอธิบายของปริพันธ์ที่ไม่แน่นอนในฟังก์ชันตรีโกณมิติธรรมดาและพิเศษ หวังว่าจะสามารถศึกษาได้ดี
อ่านเพิ่มเติม: บรรทัดฐานของความเหมาะสม: คำจำกัดความวัตถุประสงค์การลงโทษและตัวอย่าง [FULL]เพื่อให้เข้าใจแนวคิดของอินทิกรัลนี้ได้ดีขึ้นคุณสามารถฝึกทำคำถามฝึกหัดได้ หากมีสิ่งที่คุณต้องการถามให้จดไว้ในคอลัมน์ความคิดเห็น
