สูตรสามเหลี่ยมของปาสคาลและตัวอย่างปัญหา

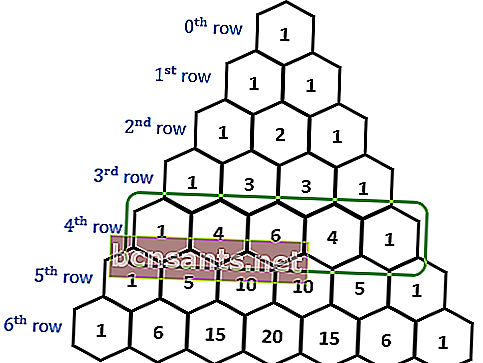
สามเหลี่ยมของปาสคาลคือการจัดเรียงของรูปสามเหลี่ยมโดยการเพิ่มองค์ประกอบที่อยู่ติดกันในแถวก่อนหน้า การจัดเรียงสามเหลี่ยมนี้ทำได้โดยการเพิ่มองค์ประกอบที่อยู่ติดกันในแถวก่อนหน้า

สมมติว่าตัวแปร a และ b รวมกันแล้วยกกำลังจาก 0 เป็นยกกำลัง 3 ผลลัพธ์คือคำอธิบายต่อไปนี้

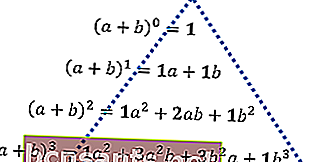
จากนั้นพิจารณาการจัดเรียงตัวเลขเป็นตัวหนาจากบนลงล่างจนกว่าคุณจะพบรูปทรงสามเหลี่ยม รูปแบบตัวเลขนี้ต่อไปนี้เรียกว่าสามเหลี่ยมปาสคาล

ทำความเข้าใจสามเหลี่ยมของปาสคาล

สามเหลี่ยมของปาสคาลคือกฎทางเรขาคณิตเกี่ยวกับสัมประสิทธิ์ทวินามของสามเหลี่ยม

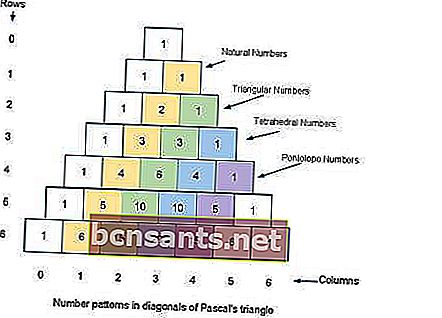
สามเหลี่ยมนี้ได้รับการตั้งชื่อตามนักคณิตศาสตร์ของ Blaise Pascal แม้ว่านักคณิตศาสตร์คนอื่น ๆ จะเคยศึกษาเรื่องนี้มาหลายศตวรรษก่อนเขาในอินเดียเปอร์เซียจีนและอิตาลี

แนวคิดของกฎ

แนวคิดของสามเหลี่ยมปาสคาลเป็นระบบการคำนวณสำหรับสามเหลี่ยมนี้โดยไม่คำนึงถึงตัวแปร a และ b ซึ่งหมายความว่าเพียงพอที่จะให้ความสนใจกับค่าสัมประสิทธิ์ทวินามดังต่อไปนี้:

1. ในบรรทัดศูนย์ให้เขียนเฉพาะตัวเลข 1
2. ในแต่ละแถวด้านล่างให้เขียนหมายเลข 1 ทางซ้ายและขวา
3. ผลรวมของตัวเลขสองตัวด้านบนแล้วเขียนในบรรทัดด้านล่าง
4. หมายเลข 1 ทางซ้ายและขวาตาม (2) ล้อมรอบผลลัพธ์เสมอ (3)
5. การคำนวณสามารถดำเนินต่อไปได้ด้วยรูปแบบเดียวกัน

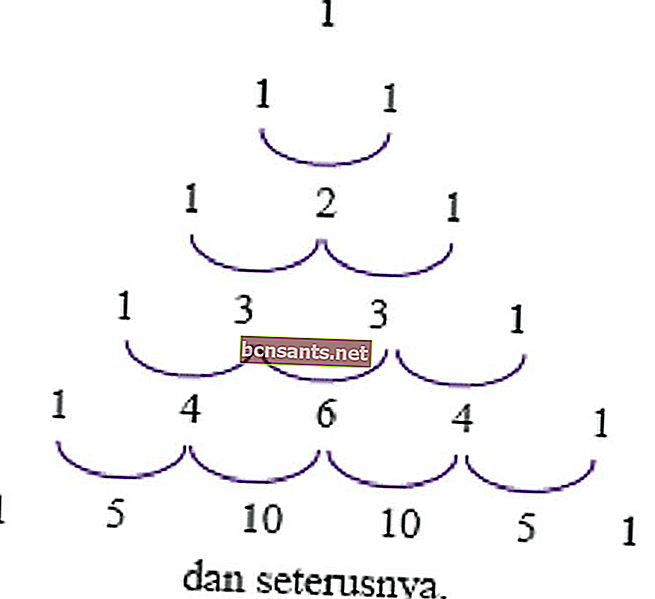
การใช้สามเหลี่ยมนี้อย่างหนึ่งคือการหาค่าสัมประสิทธิ์กำลัง (a + b) หรือ (ab) เพื่อให้มีประสิทธิภาพมากขึ้น การใช้งานนี้อธิบายไว้ในตัวอย่างต่อไปนี้

ตัวอย่างปัญหา

คำแนะนำ: ให้ความสนใจกับสามเหลี่ยมของ Pascal

1. คำแปล (a + b) 4 คืออะไร?

วิธีแก้ไข : สำหรับ (a + b) 4

• ขั้นแรกให้จัดเรียงตัวแปร a และ b โดยเริ่มจาก a4b หรือ a4
• จากนั้นพลังของลดลงเป็น 3 ซึ่งก็คือ a3b1 (ผลรวมของพลัง ab ต้องเป็น 4)
• จากนั้นพลังลดลงเหลือ 2 กลายเป็น a2b2
• จากนั้นพลังลดลงเหลือ 1 กลายเป็น ab3
• จากนั้นพลังลดลงเหลือ 0 ถึง b4
• จากนั้นเขียนสมการที่มีค่าสัมประสิทธิ์หน้าว่าง

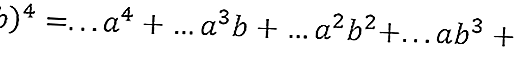
ตามรูปที่ 2 ในลำดับที่ 4 จะได้รับตัวเลข 1,4,6,4,1 ดังนั้นการแปล (a + b) 4 จะได้รับ

2. สัมประสิทธิ์ a3b3 ที่ (a + b) 6 คืออะไร?

อ่านเพิ่มเติม: วัสดุสนามแม่เหล็ก: สูตรตัวอย่างปัญหาและคำอธิบาย

วิธีแก้ไข :

จากคำถามข้อที่ 1 ลำดับของตัวแปรจาก (a + b) 6 ถูกจัดเรียงคือ

a6, a5b1, a4b2, ก3 b 3 .

ซึ่งหมายความว่าในสถานที่ที่สี่ (รูปที่ 2 ลำดับ 6) ในรูปแบบที่ 1, 6, 15, 20เป็น20 ดังนั้นจึงสามารถเขียน a3b3 ได้ 20

3. กำหนดคำแปลของ (3a + 2b) 3

การตั้งถิ่นฐาน

สูตรทั่วไปสำหรับสามเหลี่ยมปาสคาลเมื่อผลรวมของตัวแปร a และ b ยกกำลัง 3 แสดงดังนี้

เมื่อเปลี่ยนตัวแปรเป็น 3a และ 2b เราจะได้