
การสร้างพื้นที่เป็นหัวข้อที่มักมีการพูดคุยกันในวิชาคณิตศาสตร์สูตรมักจะเป็นปัญหาทางคณิตศาสตร์ในระดับประถมศึกษาและมัธยมศึกษาตอนต้น
พื้นที่อาคารสามารถตีความได้ว่าเป็นอาคารที่มีปริมาตรหรือเนื้อหาทางคณิตศาสตร์ นอกจากนี้ยังสามารถตีความได้ว่ารูปร่างของช่องว่างเป็นรูปทรงสามมิติที่มีปริมาตรหรือช่องว่างและถูก จำกัด ด้วยด้านข้าง
มีรูปแบบต่างๆของช่องว่างเช่นบล็อกลูกบาศก์ท่อลูกบอลและอื่น ๆ
แต่ละรูปร่างเหล่านี้มีสูตรสำหรับปริมาตรและพื้นที่ผิวตามลำดับ บางครั้งสิ่งนี้ทำให้นักเรียนจำได้ยาก
ที่นี่ฉันได้จัดทำรายการสูตรการสร้างทั้งหมดเพื่อให้คุณสามารถแก้ปัญหาทางคณิตศาสตร์ต่างๆในเรื่องนี้ได้อย่างง่ายดาย
1. ลูกบาศก์
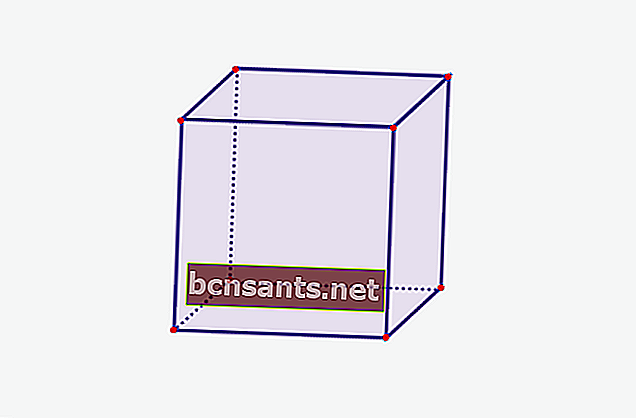
| ปริมาตรของลูกบาศก์ | V = sxsxs |
| พื้นที่ผิวของลูกบาศก์ | L = 6 x (sxs) |
| วงกลมลูกบาศก์ | K = 12 xs |
| พื้นที่ด้านหนึ่ง | L = sxs |
2. คาน
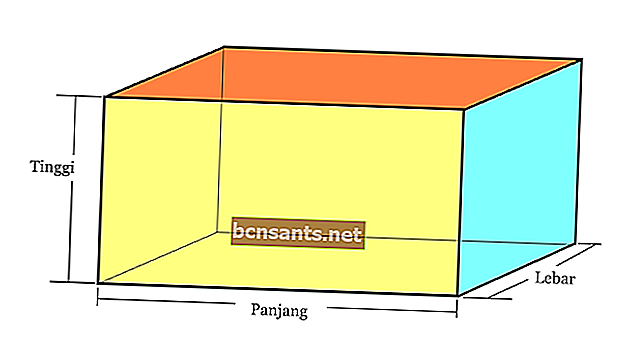
| บล็อกปริมาณ | V = pxlxt |
| ปิดกั้นพื้นที่ผิว | L = 2 x (pl + lt + จุด) |
| ช่องว่างในแนวทแยง | ง = √ ( p2 + l2 + t2) |
| เส้นรอบวงของลำแสง | K = 4 x (กว้าง + l + h) |
3. ปริซึมสามเหลี่ยม
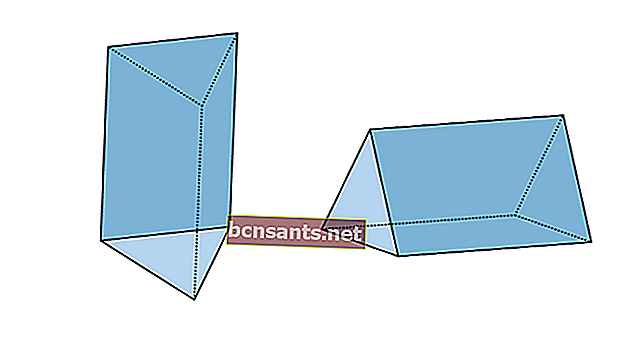
| ปริมาตรของปริซึมสามเหลี่ยม | V = พื้นที่ของฐาน xt |
| พื้นที่ผิวของปริซึมสามเหลี่ยม | L = ปริมณฑลของฐาน xt + พื้นที่ 2 x ของฐานของสามเหลี่ยม |
4. รูปสี่เหลี่ยมที่ห้า
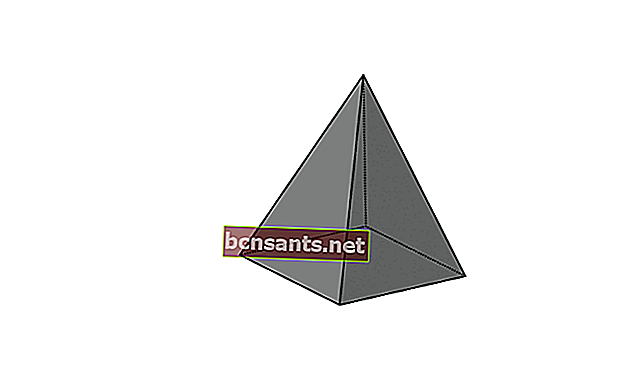
| ปริมาตรของปิรามิด | V = 1/3 xpxlxt |
| พื้นที่ผิวของพีระมิด | L = พื้นที่ของฐาน + พื้นที่ของท่อพีระมิด |
5. สามเหลี่ยมที่ห้า
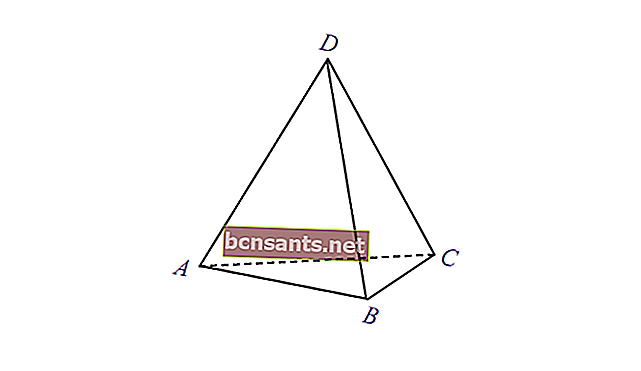
| ปริมาตรของปิรามิด | V = 1/3 x พื้นที่ของฐาน xt |
| พื้นที่ผิว | L = พื้นที่ของฐาน + พื้นที่ของท่อพีระมิด |
6. หลอด

| ปริมาณหลอด | V = π x r2 xt |
| พื้นที่ผิวท่อ | L = (พื้นที่ 2 x ของฐาน) + (ปริมณฑลของฐาน x สูง) |
7. โคน

| ปริมาณกรวย | V = 1/3 x π x r2 xt |
| พื้นที่ผิวของกรวย | A = (π x r2) + (π xrxs) |
8. ลูกบอล

| ปริมาณบอล | V = 4/3 x π x r3 |
| พื้นที่ผิวของลูกบอล | ก = 4 x π x r2 |
ตารางสูตรการสร้างที่สมบูรณ์
นอกจากนี้คุณยังสามารถรับรายการด้านบนสั้น ๆ ได้โดยดูที่ตารางด้านล่าง คุณยังสามารถบันทึกภาพนี้เพื่อให้กลับมาดูอีกครั้งได้ทุกเมื่อ
นี่คือคำอธิบายของสูตรการสร้างแบบฟอร์มสำหรับคำนวณปริมาตรและพื้นที่ผิว
หวังว่าคำอธิบายข้างต้นจะช่วยให้คุณเข้าใจรูปร่างของพื้นที่เพื่อให้คุณสามารถใช้ในการแก้ปัญหาทางคณิตศาสตร์และการใช้งานต่างๆในชีวิตประจำวัน
ข้อมูลอ้างอิง
- การทบทวนสูตรปริมาตร - Khan Academy
- แผ่นสูตรเรขาคณิต
